
 +λ2
+λ2 +λ3
+λ3 =
= ,则三个角∠AOB、∠BOC、∠COA
,则三个角∠AOB、∠BOC、∠COA +λ2
+λ2 +λ3
+λ3 =
= ,移向得λ1
,移向得λ1 +λ2
+λ2 =-λ3
=-λ3 ,两边同时点乘
,两边同时点乘 ,得λ1
,得λ1 •
• +λ2
+λ2
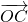 =-λ3
=-λ3
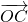 <0,在根据正实数λ1﹑λ2﹑λ3,和向量数量积的定义即可确定∠BOC、∠COA至少有一个为钝角,同理可证明∠AOB、∠BOC至少有一个为钝角,∠AOB、∠COA至少有一个为钝角,从而得到结论.
<0,在根据正实数λ1﹑λ2﹑λ3,和向量数量积的定义即可确定∠BOC、∠COA至少有一个为钝角,同理可证明∠AOB、∠BOC至少有一个为钝角,∠AOB、∠COA至少有一个为钝角,从而得到结论. +λ2
+λ2 +λ3
+λ3 =
= ,
, +λ2
+λ2 =-λ3
=-λ3 ,两边同时点乘
,两边同时点乘 ,得
,得 •
• +λ2
+λ2
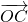 =-λ3
=-λ3
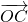 ,
, |•|
|•| |cos∠COA+λ2
|cos∠COA+λ2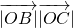 cos∠BOC=-λ3
cos∠BOC=-λ3
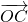 <0,,
<0,,

科目:高中数学 来源: 题型:
 给出下列四个命题:
给出下列四个命题:| π |
| 6 |
| 5 |
| 6 |
| OA |
| OB |
| OC |
| ||
|
| 1 |
| 12 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| OA |
| OB |
| OC |
| 0 |
| A、都是锐角 |
| B、至多有两个钝角 |
| C、恰有两个钝角 |
| D、至少有两个钝角 |
查看答案和解析>>
科目:高中数学 来源:2010-2011学年安徽省六安一中高三(下)第七次月考数学试卷(理科)(解析版) 题型:填空题
 ;
; ,则α+β=1是A、B、C三点共线的充要条件;
,则α+β=1是A、B、C三点共线的充要条件; (p为正常数,n∈N*),则称数列an是“等方比数列”.根据此定义可以断定:若数列an是“等方比数列”,则它一定是等比数列;
(p为正常数,n∈N*),则称数列an是“等方比数列”.根据此定义可以断定:若数列an是“等方比数列”,则它一定是等比数列;

查看答案和解析>>
科目:高中数学 来源:2012年上海市黄浦区、嘉定区高考数学二模试卷(理科)(解析版) 题型:选择题
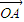 +λ2
+λ2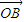 +λ3
+λ3 =
= ,则三个角∠AOB、∠BOC、∠COA( )
,则三个角∠AOB、∠BOC、∠COA( )查看答案和解析>>
科目:高中数学 来源:2011年重庆十一中高考数学一模训练试卷(二)(解析版) 题型:选择题
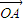 +λ2
+λ2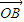 +λ3
+λ3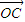 =
=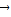 ,则三个角∠AOB、∠BOC、∠COA( )
,则三个角∠AOB、∠BOC、∠COA( )查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com