
在ΔABC中,顶点A,B, C所对三边分别是a,b,c已知B(-1, 0), C(1, 0),且b,a, c成等差数列.
(I )求顶点A的轨迹方程;
(II) 设顶点A的轨迹与直线y=kx+m相交于不同的两点M、N,如果存在过点P(0,-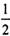 )的直线l,使得点M、N关于l对称,求实数m的取值范围
)的直线l,使得点M、N关于l对称,求实数m的取值范围
(1)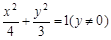 (2)当k=0时,m的取值范围为
(2)当k=0时,m的取值范围为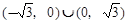 ;
;
当k≠0时,m的取值范围为(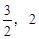 ).
).
【解析】(I ) 且b,a, c成等差数列结合椭圆的定义求得轨迹方程;(II)将y=kx+m与椭圆方程联立,判别式大于0,根据点关于直线对称,得k、m的关系
解:(I)由题知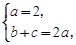 得b+c=4,即|AC|+|AB|=4(定值).
得b+c=4,即|AC|+|AB|=4(定值).
由椭圆定义知,顶点A的轨迹是以B、C为焦点的椭圆(除去左右顶点),
且其长半轴长为2,半焦距为1,于是短半轴长为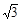 .
.
∴
顶点A的轨迹方程为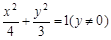 .………………………………4分
.………………………………4分
(II)由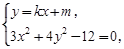
消去y整理得(3+4k2)x2+8kmx+4(m2-3)=0.∴ Δ=(8km)2-4(3+4k2)×4(m2-3)>0,
整理得:4k2>m2-3.①令M(x1,y1),N(x2,y2),则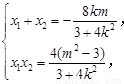
设MN的中点P(x0,y0),则
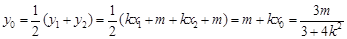 ,…………………7分
,…………………7分
i)当k=0时,由题知,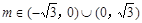 .……………………………8分
.……………………………8分
ii)当k≠0时,直线l方程为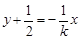 ,由P(x0,y0)在直线l上,得
,由P(x0,y0)在直线l上,得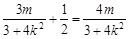 ,得2m=3+4k2.②把②式代入①中可得2m-3>m2-3,解得0<m<2.又由②得2m-3=4k2>0,解得
,得2m=3+4k2.②把②式代入①中可得2m-3>m2-3,解得0<m<2.又由②得2m-3=4k2>0,解得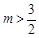 .∴
.∴ 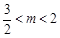 .验证:当(-2,0)在y=kx+m上时,得m=2k代入②得4k2-4k+3=0,k无解.即y=kx+m不会过椭圆左顶点.同理可验证y=kx+m不过右顶点.∴ m的取值范围为(
.验证:当(-2,0)在y=kx+m上时,得m=2k代入②得4k2-4k+3=0,k无解.即y=kx+m不会过椭圆左顶点.同理可验证y=kx+m不过右顶点.∴ m的取值范围为(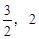 ).………11分
).………11分
综上,当k=0时,m的取值范围为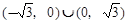 ;当k≠0时,m的取值范围为(
;当k≠0时,m的取值范围为(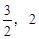 ).
).


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
| CM |
| CN |
| CM |
| CN |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 | 2 |
查看答案和解析>>
科目:高中数学 来源:2011-2012学年河南郑州高三第一次质量预测理数学试卷(解析版) 题型:解答题
在△ABC中,顶点A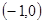 ,B
,B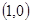 ,动点D,E满足:①
,动点D,E满足:①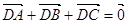 ;②
;②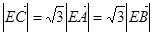 ,③
,③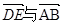 共线.
共线.
(Ⅰ)求△ABC顶点C的轨迹方程;
(Ⅱ)是否存在圆心在原点的圆,只要该圆的切线与顶点C的轨迹有两个不同交点M,N,就一定有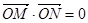 ,若存在,求该圆的方程;若不存在,请说明理由.
,若存在,求该圆的方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年河南郑州高三第一次质量预测文科数学试卷(解析版) 题型:解答题
在△ABC中,顶点A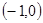 ,B
,B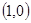 ,动点D,E满足:①
,动点D,E满足:①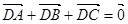 ;②
;②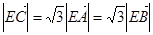 ,③
,③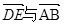 共线.
共线.
(Ⅰ)求△ABC顶点C的轨迹方程;
(Ⅱ)若斜率为1直线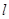 与动点C的轨迹交与M,N两点,且
与动点C的轨迹交与M,N两点,且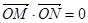 ,求直线
,求直线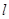 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年河南省镇平一高高三下学期第四次周考文科数学试卷 题型:解答题
.(本小题满分12分)
在△ABC中,顶点A(-1,0),B(1,0),动点D,E满足:
①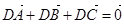 ;②|
;②|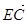 |=
|=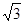 |
|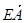 |=
|=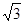 |
|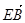 |③
|③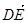 与
与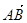 共线.
共线.
(Ⅰ)求△ABC顶点C的轨迹方程;
(Ⅱ)
若斜率为1直线l与动点C的轨迹交于M,N两点,且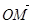 ·
·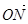 =0,求直线l的方程.
=0,求直线l的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com