
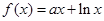
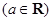 .
.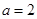 ,求曲线
,求曲线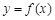 在
在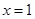 处切线的斜率;
处切线的斜率; 的单调区间;
的单调区间;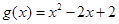 ,若对任意
,若对任意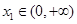 ,均存在
,均存在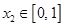 ,使得
,使得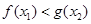 ,求
,求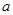 的取值范围。
的取值范围。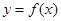 在
在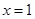 处切线的斜率为
处切线的斜率为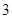 .
.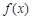 的单调递增区间为
的单调递增区间为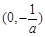 ,单调递减区间为
,单调递减区间为 .
.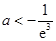 .
. 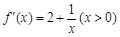 ,…………………………(2分)
,…………………………(2分)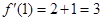 .故曲线
.故曲线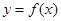 在
在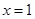 处切线的斜率为
处切线的斜率为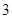 .……………(4分)
.……………(4分)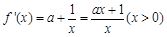 .………………………(5分)
.………………………(5分)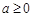 时,由于
时,由于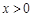 ,故
,故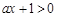 ,
,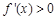
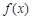 的单调递增区间为
的单调递增区间为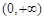 .…………………………(6分)
.…………………………(6分)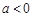 时,由
时,由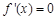 ,得
,得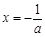 .在区间
.在区间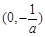 上,
上,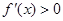 ,在区间
,在区间 上
上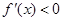 ,
,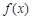 的单调递增区间为
的单调递增区间为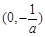 ,单调递减区间为
,单调递减区间为 .…(8分)
.…(8分) .……………………………(9分)
.……………………………(9分)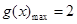 …………………………………………(10分)
…………………………………………(10分)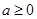 时,
时,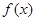 在
在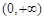 上单调递增,值域为
上单调递增,值域为 ,故不符合题意.
,故不符合题意.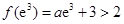 ,故不符合题意.)……………(11分)
,故不符合题意.)……………(11分) 时,
时,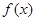 在
在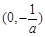 上单调递增,在
上单调递增,在 上单调递减,
上单调递减,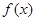 的极大值即为最大值,
的极大值即为最大值,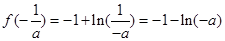 ,……(13分)
,……(13分)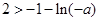 解得
解得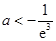 . ……………………(14分)
. ……………………(14分)

科目:高中数学 来源:不详 题型:单选题
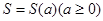 是图1中阴影部分介于平等线
是图1中阴影部分介于平等线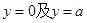 之间的那一部分的面积,则函数
之间的那一部分的面积,则函数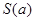 的图象大致为( )
的图象大致为( )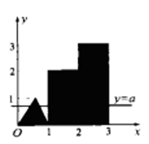
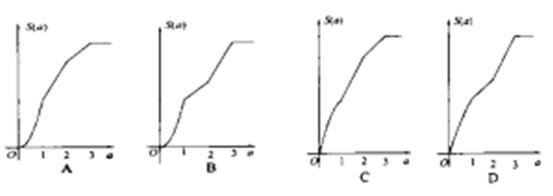
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com