
【题目】如果定义在R上的函数f(x)满足:对于任意x1≠x2 , 都有xlf(xl)+x2f(x2)≥xlf(x2)+x2f(xl),则称f(x)为“H函数”,给出下列函数: ①y=﹣x3+x+l;
②y=3x﹣2(sinx﹣cosx);
③y=l﹣ex;
④f(x)= ![]() ;
;
⑤y= ![]()
其中“H函数”的个数有( )
A.3个
B.2个
C.l个
D.0个
【答案】B
【解析】解:根据题意,对于x1f(x1)+x2f(x2)≥x1f(x2)+x2f(x1), 则有f(x1)(x1﹣x2)﹣f(x2)(x1﹣x2)≥0,
即[f(x1)﹣f(x2)](x1﹣x2)≥0,
分析可得:若函数f(x)为“H函数”,则函数f(x)为增函数或常数函数;
对于①、y=﹣x3+x+l,有y′=﹣3x2+l,不是增函数也不是常数函数,则其不是“H函数”,
对于②、y=3x﹣2(sinx﹣cosx);有y′=3﹣2(sinx+cosx)=3﹣2 ![]() sin(x+
sin(x+ ![]() ),有y′≥0,
),有y′≥0,
y=3x﹣2(sinx﹣cosx)为增函数,则其是“H函数”,
对于③、y=l﹣ex=﹣ex+1,是减函数,则其不是“H函数”,
对于④、f(x)= ![]() ,当x<1时是常数函数,当x≥1时是增函数,则其是“H函数”,
,当x<1时是常数函数,当x≥1时是增函数,则其是“H函数”,
对于⑤、y= ![]() ,当x≠0时,y=
,当x≠0时,y= ![]() ,当x>1和x<﹣1时,函数为减函数,故其不是增函数也不是常数函数,则其不是“H函数”,
,当x>1和x<﹣1时,函数为减函数,故其不是增函数也不是常数函数,则其不是“H函数”,
综合可得:有2个是“H函数”,
故选:B.
【考点精析】认真审题,首先需要了解函数单调性的判断方法(单调性的判定法:①设x1,x2是所研究区间内任两个自变量,且x1<x2;②判定f(x1)与f(x2)的大小;③作差比较或作商比较).


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知△ABC中,a,b,c分别为角A,B,C的对边,csinC﹣asinA=( ![]() c﹣b)sinB.
c﹣b)sinB.
(Ⅰ)求角A;
(Ⅱ)若a=1,求三角形ABC面积S的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在△ABC中,M是边BC的中点,tan∠BAM= ![]() ,cos∠AMC=﹣
,cos∠AMC=﹣ ![]() (Ⅰ)求角B的大小;
(Ⅰ)求角B的大小;
(Ⅱ)若角∠BAC= ![]() ,BC边上的中线AM的长为
,BC边上的中线AM的长为 ![]() ,求△ABC的面积.
,求△ABC的面积.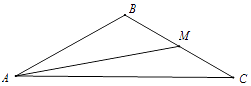
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)在(m,n)上的导函数为g(x),x∈(m,n),g(x)若的导函数小于零恒成立,则称函数f(x)在(m,n)上为“凸函数”.已知当a≤2时, ![]() ,在x∈(﹣1,2)上为“凸函数”,则函数f(x)在(﹣1,2)上结论正确的是( )
,在x∈(﹣1,2)上为“凸函数”,则函数f(x)在(﹣1,2)上结论正确的是( )
A.既有极大值,也有极小值
B.有极大值,没有极小值
C.没有极大值,有极小值
D.既无极大值,也没有极小值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ex+ax+b(a,b∈R)在x=ln2处的切线方程为y=x﹣2ln2. (Ⅰ)求函数f(x)的单调区间;
(Ⅱ)若k为差数,当x>0时,(k﹣x)f'(x)<x+1恒成立,求k的最大值(其中f'(x)为f(x)的导函数).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆E的方程为 ![]() +y2=1(a>1),O为坐标原点,直线l与椭圆E交于点A,B,M为线段AB的中点.
+y2=1(a>1),O为坐标原点,直线l与椭圆E交于点A,B,M为线段AB的中点.
(1)若A,B分别为E的左顶点和上顶点,且OM的斜率为﹣ ![]() ,求E的标准方程;
,求E的标准方程;
(2)若a=2,且|OM|=1,求△AOB面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市为了鼓励市民节约用电,实行“阶梯式”电价,将该市每户居民的月用电量划分为三档,月用电量不超过200度的部分按0.5元/度收费,超过200度但不超过400度的部分按0.8元/度收费,超过400度的部分按1.0元/度收费.
(1)求某户居民用电费用 ![]() (单位:元)关于月用电量
(单位:元)关于月用电量 ![]() (单位:度)的函数解析式;
(单位:度)的函数解析式;
(2)为了了解居民的用电情况,通过抽样,获得了今年1月份100户居民每户的用电量,统计分析后得到如图所示的频率分布直方图,若这100户居民中,今年1月份用电费用不超过260元的占80%,求 ![]() 的值;
的值;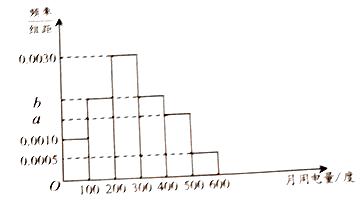
(3)在满足(2)的条件下,估计1月份该市居民用户平均用电费用(同一组中的数据用该组区间的中点值作代表).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在三棱柱ABC﹣A1B1C1中,B1B⊥平面ABC,∠ABC=90°,B1B=AB=2BC=4,D、E分别是B1C1 , A1A的中点. 
(1)求证:A1D∥平面B1CE;
(2)设M是的中点,N在棱AB上,且BN=1,P是棱AC上的动点,直线NP与平面MNC所成角为θ,试问:θ的正弦值存在最大值吗?若存在,请求出 ![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义域为R的函数 f (x)的导函数为f'(x),且满足f'(x)﹣2f (x)>4,若 f (0)=﹣1,则不等式f(x)+2>e2x的解集为( )
A.(0,+∞)
B.(﹣1,+∞)
C.(﹣∞,0)
D.(﹣∞,﹣1)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com