
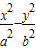 =1(a>0,b>0)上任意一点P引实轴平行线交两渐近线于Q,R两点,则|PQ|•|PR|之值为 .
=1(a>0,b>0)上任意一点P引实轴平行线交两渐近线于Q,R两点,则|PQ|•|PR|之值为 . 科目:高中数学 来源:2010年重庆市部分重点中学高高考数学一模试卷(理科)(解析版) 题型:选择题
 =1(a>0,b>0)的右顶点为A,P为双曲线上的一个动点(不是顶点),从点A引双曲线的两条渐近线的平行线,与直线OP分别交于Q,R两点,其中O为坐标原点,则|OP|2与|OQ|•|OR|的大小关系为( )
=1(a>0,b>0)的右顶点为A,P为双曲线上的一个动点(不是顶点),从点A引双曲线的两条渐近线的平行线,与直线OP分别交于Q,R两点,其中O为坐标原点,则|OP|2与|OQ|•|OR|的大小关系为( )查看答案和解析>>
科目:高中数学 来源:2011年江苏省淮安市清河区清江中学高考数学押题卷(解析版) 题型:解答题
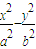 =1(a>0,b>0)的左焦点F引圆x2+y2=a2的切线,切点为T,延长 FT交双曲线右支于P点,若M为线段FP的中点,O为坐标原点,则|MO|-|MT| b-a(填“大于、小于、等于或不确定”)
=1(a>0,b>0)的左焦点F引圆x2+y2=a2的切线,切点为T,延长 FT交双曲线右支于P点,若M为线段FP的中点,O为坐标原点,则|MO|-|MT| b-a(填“大于、小于、等于或不确定”)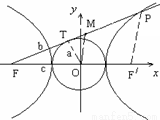
查看答案和解析>>
科目:高中数学 来源:2009-2010学年湖北省“黄冈中学、黄石二中、华师一附中、荆州中学、孝感高中、襄樊四中、襄樊五中、鄂南高中”八校高三第一次联考数学试卷(理科)(解析版) 题型:选择题
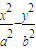 =1(a>0,b>0)的右顶点为A,P为双曲线上的一个动点(不是顶点),从点A引双曲线的两条渐近线的平行线,与直线OP分别交于Q,R两点,其中O为坐标原点,则|OP|2与|OQ|•|OR|的大小关系为( )
=1(a>0,b>0)的右顶点为A,P为双曲线上的一个动点(不是顶点),从点A引双曲线的两条渐近线的平行线,与直线OP分别交于Q,R两点,其中O为坐标原点,则|OP|2与|OQ|•|OR|的大小关系为( )查看答案和解析>>
科目:高中数学 来源:2010年重庆市重点高中高考数学三模试卷(理科)(解析版) 题型:选择题
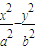 =1(a>0,b>0)的右顶点为A,P为双曲线上的一个动点(不是顶点),从点A引双曲线的两条渐近线的平行线,与直线OP分别交于Q,R两点,其中O为坐标原点,则|OP|2与|OQ|•|OR|的大小关系为( )
=1(a>0,b>0)的右顶点为A,P为双曲线上的一个动点(不是顶点),从点A引双曲线的两条渐近线的平行线,与直线OP分别交于Q,R两点,其中O为坐标原点,则|OP|2与|OQ|•|OR|的大小关系为( )查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com