
从曲线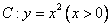 上一点
上一点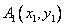 引曲线C的第一条切线
引曲线C的第一条切线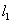 ,
,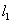 交
交 轴于点
轴于点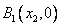 ,过点
,过点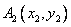 引曲线C的第二条切线
引曲线C的第二条切线 ,
, 交
交 轴于点
轴于点 ,…如此反复作下去,由切线
,…如此反复作下去,由切线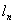 得到点列
得到点列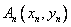 ,
,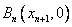 ,
,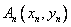 的横坐标组成数列
的横坐标组成数列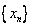 ,
,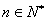
(1)若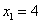 ,求数列
,求数列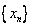 的通项公式;
的通项公式;
(2)若对于任意的正整数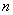 都有
都有 恒成立,且
恒成立,且 ,求
,求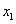 的最大值;
的最大值;
(3)在(1)的条件下,记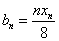 ,数列
,数列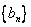 的前
的前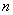 项和为
项和为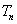 ,试比较
,试比较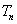 与1的大小。
与1的大小。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com