
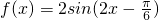 ,x∈R.
,x∈R. 上的最大值和最小值.
上的最大值和最小值.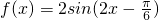 ,x∈R中,令 2x-
,x∈R中,令 2x- =kπ+
=kπ+ ,k∈z,可得
,k∈z,可得 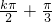 ,故函数f(x)的对称轴方程为 x=
,故函数f(x)的对称轴方程为 x=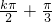 ,k∈z.
,k∈z. =kπ,k∈z,可得 x=
=kπ,k∈z,可得 x= ,故对称轴中心的坐标为(
,故对称轴中心的坐标为( ,0),k∈z.
,0),k∈z. ≤2x-
≤2x- ≤2kπ+
≤2kπ+ ,k∈z,解得 kπ-
,k∈z,解得 kπ- ≤x≤kπ+
≤x≤kπ+ ,
, ,kπ+
,kπ+ ],k∈z.
],k∈z. ≤2x-
≤2x- ≤2kπ+
≤2kπ+ ,k∈z,解得 kπ+
,k∈z,解得 kπ+ ≤x≤kπ+
≤x≤kπ+ ,
, ,kπ+
,kπ+ ],k∈z.
],k∈z. ,∴-
,∴- ≤2x-
≤2x- ≤
≤ ,故当 x=
,故当 x= 时,函数f(x)的最大值为2,
时,函数f(x)的最大值为2, 时,函数f(x)的最小值为2×(
时,函数f(x)的最小值为2×( )=-1.
)=-1.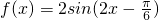 ,x∈R中,令 2x-
,x∈R中,令 2x- =kπ+
=kπ+ ,k∈z,可得称轴方程;令 2x-
,k∈z,可得称轴方程;令 2x- =kπ,可得对称轴中心的横坐标 x的值;由 2kπ-
=kπ,可得对称轴中心的横坐标 x的值;由 2kπ- ≤2x-
≤2x- ≤2kπ+
≤2kπ+ ,k∈z,解得x的范围即得增区间;令2kπ+
,k∈z,解得x的范围即得增区间;令2kπ+ ≤2x-
≤2x- ≤2kπ+
≤2kπ+ ,k∈z,解得x的范围即得减区间.
,k∈z,解得x的范围即得减区间. ≤2x-
≤2x- ≤
≤ ,利用正弦函数的单调性求得最值.
,利用正弦函数的单调性求得最值.

 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案科目:高中数学 来源:2012-2013学年广东省江门市新会一中高三(上)第四次检测数学试卷(理科)(解析版) 题型:解答题
 ,x∈R,且
,x∈R,且
 ,
, ,
, ,求cos(α+β)的值.
,求cos(α+β)的值.查看答案和解析>>
科目:高中数学 来源:2010-2011学年贵州省遵义市遵义四中高一(上)期末数学试卷(解析版) 题型:解答题
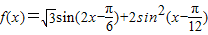 (x∈R).
(x∈R).查看答案和解析>>
科目:高中数学 来源:2010-2011学年广东省汕尾市陆丰东海中学高二(上)期末数学试卷(文科)(解析版) 题型:解答题
 ,x∈R
,x∈R
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com