
已知函数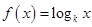 (
(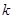 为常数,
为常数,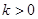 且
且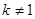 ),且数列
),且数列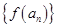 是首项为4,公差为2的等差数列。
是首项为4,公差为2的等差数列。
(Ⅰ)求证:数列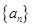 是等比数列;
是等比数列;
(Ⅱ)若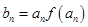 ,当
,当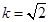 时,求数列
时,求数列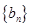 的前n项和
的前n项和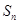 。
。
(Ⅰ)详见解析;(Ⅱ) .
.
【解析】
试题分析:(Ⅰ)数列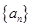 是等比数列,只需证明
是等比数列,只需证明 等于一个与
等于一个与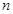 无关的常数即可,由已知数列
无关的常数即可,由已知数列 是首项为4,公差为2的等差数列,故
是首项为4,公差为2的等差数列,故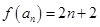 ,即
,即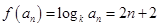 ,可求得
,可求得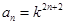 ,代入
,代入 即可数列
即可数列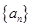 是等比数列;(Ⅱ)若
是等比数列;(Ⅱ)若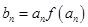 ,当
,当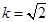 时,求数列
时,求数列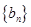 的前
的前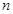 项和
项和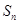 ,首先求出数列
,首先求出数列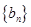 的通项公式,由(Ⅰ)可知
的通项公式,由(Ⅰ)可知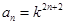 ,故
,故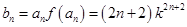 ,这是一个等差数列与一个等比数列对应项积所组成的数列,可利用错位相减法来求和,可求得
,这是一个等差数列与一个等比数列对应项积所组成的数列,可利用错位相减法来求和,可求得 .
.
试题解析:(Ⅰ)由题意知f(an)=4+(n-1)×2=2n+2, (2分)
即logkan=2n+2,∴an=k2n+2, (3分)
∴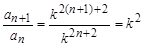 .
(5分)
.
(5分)
∵常数k>0且k≠1,∴k2为非零常数,
∴数列{an}是以k4为首项,k2为公比的等比数列。 (6分)
(Ⅱ)由(1)知,bn=anf(an)=k2n+2·(2n+2),
当k=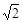 时,bn=(2n+2)·2n+1=(n+1)·2n+2.
(8分)
时,bn=(2n+2)·2n+1=(n+1)·2n+2.
(8分)
∴Sn=2·23+3·24+4·25++(n+1)·2n+2, ①
2Sn=2·24+3·25++n·2n+2+(n+1)·2n+3, ② (10分)
②-①,得Sn=―2·23―24―25――2n+2+(n+1)·2n+3
=―23―(23+24+25++2n+2)+(n+1)·2n+3,
∴Sn=―23― +(n+1)·2n+3=n·2n+3.
(12分)
+(n+1)·2n+3=n·2n+3.
(12分)
考点:等差数列与等比数列的综合,数列求和.


 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案科目:高中数学 来源: 题型:
已知函数![]() (
(![]() 为常数,且
为常数,且![]() )的图象过点
)的图象过点![]() ,且函数
,且函数![]() 的最大值为2。
的最大值为2。
(1)、求函数![]() 的解析式,并写出其单调递增区间。
的解析式,并写出其单调递增区间。
(2)、若函数![]() 的图象按向量
的图象按向量![]() 作移动距离最小的平移后,使所的图象关于y轴对称,求出向量
作移动距离最小的平移后,使所的图象关于y轴对称,求出向量![]() 的坐标及平移后的图象对应的函数解析式。
的坐标及平移后的图象对应的函数解析式。
查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数![]() 、
、![]() 为 常数,且
为 常数,且![]() )的图象过 点(0,
)的图象过 点(0,![]() ),且函数
),且函数![]() 的最大值为2。
的最大值为2。
⑴求函数![]() 的解析式,并写出其单调递增区间;
的解析式,并写出其单调递增区间;
⑵若函数![]() 的图象按向量
的图象按向量![]() 作移动距离最小的平移后,使所得图象关于
作移动距离最小的平移后,使所得图象关于![]() 轴对称,求出向量
轴对称,求出向量![]() 的坐标及平移后的图象对应的函数解析式.
的坐标及平移后的图象对应的函数解析式.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年浙江省高三第二次阶段性考试数学试卷(解析版) 题型:选择题
已知函数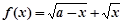 (
(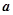 为常数,且
为常数,且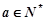 ),对于定义域内的任意两个实数
),对于定义域内的任意两个实数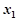 、
、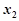 ,恒有
,恒有 成立,则正整数
成立,则正整数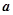 可以取的值有
可以取的值有
A.4个 B.5个 C.6 个 D.7个
查看答案和解析>>
科目:高中数学 来源:2012-2013学年浙江省高三10月阶段性测试理科数学试卷(解析版) 题型:选择题
已知函数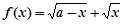 (
(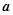 为常数,且
为常数,且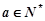 ),对于定义域内的任意两个实数
),对于定义域内的任意两个实数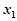 、
、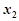 ,恒有
,恒有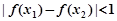 成立,则正整数
成立,则正整数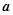 可以取的值有
可以取的值有
A.4个 B.5个 C.6 个 D.7个
查看答案和解析>>
科目:高中数学 来源:2010年广东省高考冲刺强化训练试卷二文科数学 题型:解答题
(本小题满分14分)
已知函数 (
(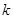 为常数,
为常数, 且
且 ),且数列
),且数列 是首项为4,
是首项为4,
公差为2的等差数列.
(Ⅰ)求证:数列 是等比数列;
是等比数列;
(Ⅱ) 若 ,当
,当 时,求数列
时,求数列 的前
的前 项和
项和 ;
;
(III)若 ,且
,且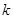 >1,比较
>1,比较 与
与 的大小.
的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com