
| h |
| tan30° |
| 3 |
| 3 |
| 6 |
| h |
| tan45° |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 6 |
| OC |
| t |
(
| ||
|
| 3 |
| 2 |
| 6 |
| 2 |
| 3 |


科目:高中数学 来源: 题型:
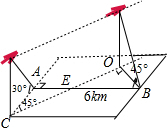
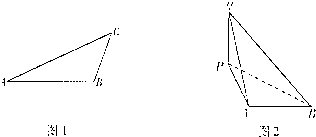 某飞船返回仓顺利返回地球后,为了及时救出航天员,地面指挥中心在返回仓预计到达的区域内安排了三个救援中心(如图1分别记为A,B,C),B地在A地正东方向上,两地相距6km; C地在B地北偏东30°方向上,两地相距4km,假设P为航天员着陆点,某一时刻A救援中心接到从P点发出的求救信号,经过4s后,B、C两个救援中心也同时接收到这一信号,已知该信号的传播速度为1km/s.
某飞船返回仓顺利返回地球后,为了及时救出航天员,地面指挥中心在返回仓预计到达的区域内安排了三个救援中心(如图1分别记为A,B,C),B地在A地正东方向上,两地相距6km; C地在B地北偏东30°方向上,两地相距4km,假设P为航天员着陆点,某一时刻A救援中心接到从P点发出的求救信号,经过4s后,B、C两个救援中心也同时接收到这一信号,已知该信号的传播速度为1km/s.查看答案和解析>>
科目:高中数学 来源: 题型:
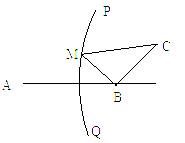 如图,B地在A地正东方向6km处,C地在
如图,B地在A地正东方向6km处,C地在
B地的北偏东30°方向2km处,河流的沿岸PQ
(曲线)上任一点到A的距离比到B的距离远
4km,现要在曲线PQ上选一处M,建一码头,
向BC两地转运货物,经测算,从M到B、M
到C修建公路费用分别是20万元/km、30万元/km,
那么修建这条路的总费用最低是
查看答案和解析>>
科目:高中数学 来源: 题型:
如图,B地在A地正东方向6km处,C地在B地的北偏东30°方向2km处,河流的沿岸PQ(曲线)上任一点到A的距离比到B的距离远4km,现要在曲线PQ上选一处M,建一码头,向BC两地转运货物,经测算,从M到B、M到C修建公路费用分别是20万元/km、30万元/km,那么修建这条路的总费用最低是
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com