
定义在R上的函数f(x)是最小正周期为2的奇函数, 且当x∈(0, 1)时,
f(x)=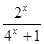 .
.
(Ⅰ)求f(x)在[-1, 1]上的解析式; (Ⅱ)证明f(x)在(0, 1)上时减函数;
(Ⅲ)当λ取何值时, 方程f(x)=λ在[-1, 1]上有解?
(1)f(x)=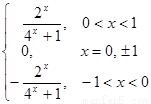 .;(2)见解析;
.;(2)见解析;
(3)λ∈(- , -
, -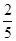 )∪{0}∪(
)∪{0}∪(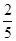 ,
,
 )时方程f(x)=λ在[-1, 1]上有解.
)时方程f(x)=λ在[-1, 1]上有解.
【解析】主要考查函数奇偶性、单调性、周期性、指数运算与指数函数的图象和性质。
解:(Ⅰ)解:当x∈(-1, 0)时, - x∈(0,
1). ∵当x∈(0, 1)时, f(x)= .
.
∴f(-x)= . 又f(x)是奇函数,
∴f (-x)= - f (x)=
. 又f(x)是奇函数,
∴f (-x)= - f (x)=  .∴f(x)= -
.∴f(x)= - .
.
∵f(-0)= -f(0), ∴f(0)= 0. 又f(x)是最小正周期为2的函数, ∴对任意的x有f(x+2)= f(x).
∴f(-1)= f(-1+2)= f(1). 另一面f(-1)=- f(1), ∴- f(1)= f(1) . ∴f(1) = f(-1)=0. ∴f(x)在[-1, 1]上的解析式为
f(x)=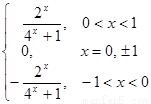 .
.
(Ⅱ) 对任意的0<x1<x2<1,f(x1)-f(x2)= -
- =
=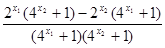 =
= =
=
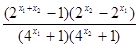 >0,因此f(x)在(0, 1)上时减函数;
>0,因此f(x)在(0, 1)上时减函数;
(Ⅲ)在[-1, 1]上使方程f(x)=λ有解的λ的取值范围就是函数f(x)在[-1,
1]上的值域. 当x∈(-1, 0)时, 2<2x+ <
< , 即2<
, 即2<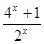 <
< . ∴
. ∴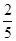 < f(x)=
< f(x)=  <
< . 又f(x)是奇函数,
∴f(x)在(-1, 0)上也是减函数, ∴当x∈(-1, 0)时有-
. 又f(x)是奇函数,
∴f(x)在(-1, 0)上也是减函数, ∴当x∈(-1, 0)时有- < f(x)= -
< f(x)= - < -
< -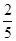 . ∴f(x)在[-1, 1]上的值域是(-
. ∴f(x)在[-1, 1]上的值域是(- , -
, -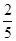 )∪{0}∪(
)∪{0}∪(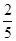 ,
,
 ).
故当
).
故当
λ∈(- , -
, -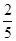 )∪{0}∪(
)∪{0}∪(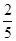 ,
,
 )时方程f(x)=λ在[-1, 1]上有解.
)时方程f(x)=λ在[-1, 1]上有解.


科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| π |
| 2 |
| π |
| 3 |
| x0 |
| 2 |
| 3 |
| 2 |
| π |
| 2 |
| π |
| 2 |
| π |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
已知定义在R上的函数f(x)的图象是连续不断的,且有如下对应值表:
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com