
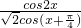 =
= ,0<x<π,则tanx为
,0<x<π,则tanx为

 ,再将此等式左右两边平方,利用同角三角函数间的基本关系化简,求出2sinxcosx的值小于0,由x的范围得到sinx大于0,cosx小于0,再利用完全平方公式及同角三角函数间的基本关系求出cosx-sinx的值,与sinx+cosx的值联立组成方程组,求出方程组的解得到sinx与cosx的值,进而确定出tanx的值.
,再将此等式左右两边平方,利用同角三角函数间的基本关系化简,求出2sinxcosx的值小于0,由x的范围得到sinx大于0,cosx小于0,再利用完全平方公式及同角三角函数间的基本关系求出cosx-sinx的值,与sinx+cosx的值联立组成方程组,求出方程组的解得到sinx与cosx的值,进而确定出tanx的值.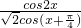 =
=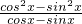 =cosx+sinx=
=cosx+sinx= ①,
①, ,即sin2x+2sinxcosx+cos2x=1+2sinxcosx=
,即sin2x+2sinxcosx+cos2x=1+2sinxcosx= ,
, <0,又0<x<π,
<0,又0<x<π, ,
, ②,
②, ,sinx=
,sinx= ,
, .
.

 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com