
 如图,矩形纸片ABCD的边AB=24,AD=25,点E、F分别在边AB与BC上.现将纸片的右下角沿EF翻折,使得顶点B翻折后的新位置B1恰好落在边AD上.设
如图,矩形纸片ABCD的边AB=24,AD=25,点E、F分别在边AB与BC上.现将纸片的右下角沿EF翻折,使得顶点B翻折后的新位置B1恰好落在边AD上.设| BE | EF |
| 24 |
| sinθ+sinθcos2θ |
| 24 |
| sinθ(1+cos2θ) |
| 24 |
| sinθ(2-2sin2θ) |
| 12 |
| sinθ(1-sin2θ) |
| π |
| 4 |
| ||
| 2 |
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
| 24 |
| sinθ+sinθcos2θ |
| 24 |
| sinθ(1+cos2θ) |
| 24 |
| sinθ(2-2sin2θ) |
| 12 |
| sinθ(1-sin2θ) |
| 12 |
| t-t3 |
| π |
| 4 |
| ||
| 2 |
| 12 |
| 25 |
| π |
| 4 |
| 3 |
| 5 |
| 3 |
| 5 |
| ||
| 2 |
| 3 |
| 5 |
| ||
| 2 |


科目:高中数学 来源: 题型:
 如图,在平面直角坐标系中,矩形纸片ABCD的长为2,宽为1.点A与坐标原点重合,AB,AD边分别在x轴、y轴的正半轴上.将矩形纸片沿直线折叠一次,使点A落在边CD上,记为点A′.
如图,在平面直角坐标系中,矩形纸片ABCD的长为2,宽为1.点A与坐标原点重合,AB,AD边分别在x轴、y轴的正半轴上.将矩形纸片沿直线折叠一次,使点A落在边CD上,记为点A′.查看答案和解析>>
科目:高中数学 来源:2013年全国普通高等学校招生统一考试理科数学(陕西卷解析版) 题型:选择题
如图, 在矩形区域ABCD的A, C两点处各有一个通信基站, 假设其信号覆盖范围分别是扇形区域ADE和扇形区域CBF(该矩形区域内无其他信号来源, 基站工作正常). 若在该矩形区域内随机地选一地点, 则该地点无信号的概率是 ( )

A.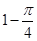 B.
B. C.
C.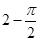 D.
D.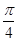
查看答案和解析>>
科目:高中数学 来源:2012-2013学年江苏省仪征市高三第一次涂卡训练数学试卷(解析版) 题型:选择题
如图,矩形纸板ABCD的顶点A、B分别在正方形边框EOFG的边OE、OF上,当点B在OF边上进行左右运动时,点A随之在OE上进行上下运动.若AB=8,BC=3,运动过程中,则点D到点O距离的最大值为

A.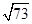 B.9 C.
B.9 C.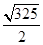 D.
D.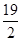
查看答案和解析>>
科目:高中数学 来源: 题型:
如图, 在矩形区域ABCD的A, C两点处各有一个通信基站, 假设其信号覆盖范围分别是扇形区域ADE和扇形区域CBF(该矩形区域内无其他信号来源, 基站工作正常). 若在该矩形区域内随机地选一地点, 则该地点无信号的概率是
(A)![]() (B)
(B)![]() (C)
(C) ![]() (D)
(D) ![]()
 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com