练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
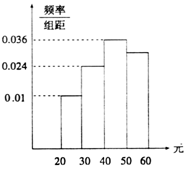
    17．为了倡导人民群众健康的生活方式，某社区服务中心通过网站对岁的社区居民随机抽取n人进行了调查，得到如下各年龄段人数频率分布直方图，若该公司决定在各年龄段用分层抽样抽取50名观众进行奖励，则年龄段[50，60]的获奖人数为（　　）
    A．10B．12C．15D．18

    分析 先由频率分布直方图计算出年龄段[50，60]的频率，进而可得年龄段[50，60]的获奖人数．

    解答 解：年龄段[50，60]的频率为：1-（0.01+0.024+0.036）×10=0.3，
    ∴年龄段[50，60]的获奖人数为50×0.3=15，
    故选：C

    点评 本题考查的知识点是频率分布直方图，分层抽样，难度不大，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    7．已知函数f（x）=|x+2|-2|x-1|．
    （1）解不等式f（x）≤1；
    （2）对于任意x∈R都有a（x+3）≥f（x）成立，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    8．已知平面向量$\overrightarrow a$，$\overrightarrow b$，$|{\overrightarrow a}|=1$，$|{\overrightarrow b}|=\sqrt{2}$，$\overrightarrow a•\overrightarrow b=1$，则向量$\overrightarrow a$，$\overrightarrow b$的夹角为（　　）
    A．$\frac{π}{6}$B．$\frac{π}{3}$C．$\frac{π}{4}$D．$\frac{π}{2}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

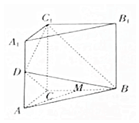    5．如图，在直三棱柱ABC-A1B1C1中，D，M分别是AA1，BC的中点，∠CDC1=90°，在△ABC中，AB=2AC，∠BAC=60°．
    （1）证明：AM∥平面BDC1；
    （2）证明：DC1⊥平面BDC．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    12．已知一家电子公司生产某种电子产品的月固定成本为20万元，每生产1千件需另投入5.4万元，设该公司一月内生产该电子产品x千件能全部销售完，每千件的销售收入为g（x）万元，且g（x）=$\left\{\begin{array}{l}{13.5-\frac{1}{30}{x}^{2}（0＜x≤10）}\\{\frac{168}{x}-\frac{2000}{3{x}^{2}}（x＞10）}\end{array}\right.$
    （Ⅰ）写出月利润y（万元）关于月产量x（千件）的函数解析式；
    （Ⅱ）月产量为多少千件时，该公司在这一产品的生产中所获利润最大？并求出最大利润．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    2．已知函数$f（x）=\frac{e^x}{e}-lnx$．
    （I）若f（x）在点（1，f（x））的切线l垂直于y轴，求切线l的方程；
    （II）求f（x）的最小值；
    （III）若关于x的不等式${e^{x-1}}+1-f（x）＞\frac{{k（{x-1}）}}{x}$在（1，+∞）恒成立，求整数k的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    9．身高互不相同的9位同学站成一排照相，并约定自中间（左数第5个位置）向两边按身高由高到低的顺序站位，若身高排第4高的同学与身高最高的同学相邻，则不同的站位顺序有20种．（用数字作答）

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    6．已知f（x）是定义在R上奇函数，又f（2）=0，若x＞0时，xf′（x）+f（x）＞0，则不等式xf（x）＞0的解集是（-∞，-2）∪（2，+∞）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    7．已知直线l：ax+y-4=0过点（-1，2），则直线l的斜率为（　　）
    A．-3B．3C．-2D．2

    查看答案和解析>>

    同步练习册答案