Question

长为L的铁棒欲水平通过宽分别为2.5米和1.28米的两个互相垂直的走廊的拐角，铁棒能通过时L的最大值为________．

Answer 1

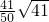
分析：设铁棒与2.5米的走廊成θ角，则可表示铁棒的长，利用导数的方法，即可求得函数的最大值．
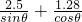
解答：设铁棒与2.5米的走廊成θ角，则L=（0＜θ＜）
∴L′=
令L′=0，可得tanθ=，∴θ=arctan
∵函数在（0，arctan）时，L′＜0单调递减，在（arctan，）时，L′＞0单调递增
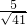
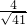
∴θ=arctan时，即sinθ=，cosθ=时，铁棒能通过时L的最大值为
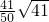
故答案为：
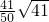
点评：本题考查函数模型的构建，考查导数知识的运用，考查学生的计算能力，属于中档题．