
【题目】设函数f(x)是定义在R上的偶函数,对任意x∈R,都有f(x)=f(x+4),且当x∈[﹣2,0]时,f(x)=( ![]() )x﹣1,若在区间(﹣2,6]内关于x的方程f(x)﹣loga(x+2)=0(a>1)恰有三个不同的实数根,则a的取值范围是( )
)x﹣1,若在区间(﹣2,6]内关于x的方程f(x)﹣loga(x+2)=0(a>1)恰有三个不同的实数根,则a的取值范围是( )
A.( ![]() ,2)
,2)
B.( ![]() ,2)
,2)
C.[ ![]() ,2)
,2)
D.( ![]() ,2]
,2]
【答案】B
【解析】解:设x∈[0,2],则﹣x∈[﹣2,0],
∴f(﹣x)=( ![]() )﹣x﹣1=2x﹣1,
)﹣x﹣1=2x﹣1,
∵f(x)是定义在R上的偶函数,
∴f(x)=f(﹣x)=2x﹣1.
∵对任意x∈R,都有f(x)=f(x+4),
∴当x∈[2,4]时,(x﹣4)∈[﹣2,0],∴f(x)=f(x﹣4)=xx﹣4﹣1;
当x∈[4,6]时,(x﹣4)∈[0,2],∴f(x)=f(x﹣4)=2x﹣4﹣1.
∵若在区间(﹣2,6]内关于x的方程f(x)﹣loga(x+2)=0(a>1)恰有三个不同的实数根,
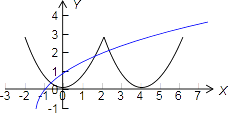
∴函数y=f(x)与函数y=loga(x+2)在区间(﹣2,6]上恰有三个交点,
通过画图可知:恰有三个交点的条件是 ![]() ,解得:
,解得: ![]() <a<2,
<a<2,
即 ![]() <a<2,因此所求的a的取值范围为(
<a<2,因此所求的a的取值范围为( ![]() ,2).
,2).
所以答案是:B
【考点精析】掌握函数奇偶性的性质是解答本题的根本,需要知道在公共定义域内,偶函数的加减乘除仍为偶函数;奇函数的加减仍为奇函数;奇数个奇函数的乘除认为奇函数;偶数个奇函数的乘除为偶函数;一奇一偶的乘积是奇函数;复合函数的奇偶性:一个为偶就为偶,两个为奇才为奇.


科目:高中数学 来源: 题型:
【题目】如图1,已知长方形ABCD中,AB=2,AD=1,E为DC的中点.将△ADE沿AE折起,使得平面ADE⊥平面ABCE. 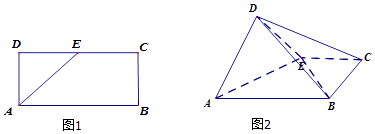
(1)求证:平面BDE⊥平面ADE
(2)求三棱锥 C﹣BDE的体积
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于函数 ![]() ,看下面四个结论( )
,看下面四个结论( )
①f(x)是奇函数;②当x>2007时, ![]() 恒成立;③f(x)的最大值是
恒成立;③f(x)的最大值是 ![]() ;④f(x)的最小值是
;④f(x)的最小值是 ![]() .其中正确结论的个数为:
.其中正确结论的个数为:
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了在夏季降温和冬季供暖时减少能源损耗,房屋的屋顶和外墙需要建造隔热层.某幢建筑物要建造可使用20年的隔热层,每厘米厚的隔热层建造成本为6万元.该建筑物每年的能源消耗费用C(单位:万元)与隔热层厚度x(单位:cm)满足关系:C(x)= ![]() (0≤x≤10),若不建隔热层,每年能源消耗费用为8万元.设f(x)为隔热层建造费用与20年的能源消耗费用之和.
(0≤x≤10),若不建隔热层,每年能源消耗费用为8万元.设f(x)为隔热层建造费用与20年的能源消耗费用之和.
(Ⅰ)求k的值及f(x)的表达式.
(Ⅱ)隔热层修建多厚时,总费用f(x)达到最小,并求最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax2+bx+c(a≠0)满足f(0)=0,对于任意x∈R都有f(x)≥x,且f(﹣ ![]() +x)=f(﹣
+x)=f(﹣ ![]() ﹣x),令g(x)=f(x)﹣|λx﹣1|(λ>0).
﹣x),令g(x)=f(x)﹣|λx﹣1|(λ>0).
(1)求函数f(x)的表达式;
(2)函数g(x)在区间(0,1)上有两个零点,求λ的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市家庭煤气的使用量x(m3)和煤气费f(x)(元) 满足关系f(x)= ![]() ,已知某家庭今年前三个月的煤气费如表:
,已知某家庭今年前三个月的煤气费如表:
月份 | 用气量 | 煤气费 |
一月份 | 4m3 | 4 元 |
二月份 | 25m3 | 14 元 |
三月份 | 35m3 | 19 元 |
若四月份该家庭使用了20m3的煤气,则其煤气费为( )元.
A.10.5
B.10
C.11.5
D.11
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在梯形ABCD中,AD∥BC,∠ABC=90°,点M、N分别在边AB、BC上,沿直线MD、DN、NM,分别将△AMD、△CDN、△BNM折起,点A,B,C重合于一点P. 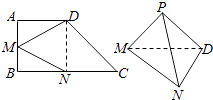
(1)证明:平面PMD⊥平面PND;
(2)若cos∠DNP= ![]() ,PD=5,求直线PD与平面DMN所成角的正弦值.
,PD=5,求直线PD与平面DMN所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设点O是平行四边形ABCD两条对角线的交点,给出下列向量组:
① ![]() 与
与 ![]() ;
;
② ![]() 与
与 ![]() ;
;
③ ![]() 与
与 ![]() ;
;
④ ![]() 与
与 ![]() .
.
其中可作为该平面其他向量基底的是( )
A.①②
B.①③
C.①④
D.③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com