
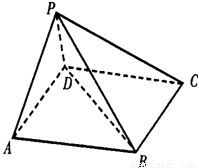
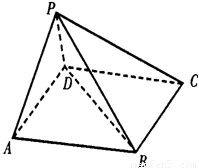
如图,在五面体P—ABCD中,底面ABCD是平行四边形,∠BAD=60°,AB=4,AD=2, PB=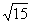 ,PD=
,PD=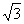 。
。
(1)求证:BD⊥平面PAD;
(2)若PD与底面ABCD成60°的角,试求二面角P—BC—A的大小。
|
(1)由已知AB=4,AD=2,∠BAD=60°,
得BD2=AD2+AB2-2AD·ABcos60°
=4+16-2×2×4× =12。∴AB2=AD2+BD2,
=12。∴AB2=AD2+BD2,
∴△ABD是直角三角形,∠ADB=90°,即AD⊥BD。
在△PDB中,PD=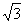 ,PB=
,PB= ,BD=
,BD= ,
,
∴PB2=PD2+BD2,故得PD⊥BD。
又PD∩AD=D,∴BD⊥平面PAD。
(2)∵BD⊥平面PAD,BD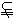 平面ABCD,
平面ABCD,
∴平面PAD⊥平面ABCD。
作PE⊥AD于E,又PE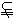 平面PAD,∴PE⊥平面ABCD,
平面PAD,∴PE⊥平面ABCD,
∴∠PDE是PD与底面BCD所成的角,∴∠PDE=60°,
∴PE=PDsin60°=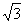 ·
· =
= 。
。
作EF⊥BC于F,连PF,则PF⊥BC,∴∠PFE是二面角P—BC—A的平面角。
又EF=BD= ,∴在Rt△PEF中,
,∴在Rt△PEF中,
tan∠PFE= =
= =
= 。
。
故二面角P—BC—A的大小为arctan 。
。


科目:高中数学 来源: 题型:
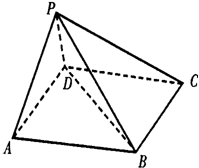 如图,在五面体P-ABCD中,底面ABCD是平行四边形,∠BAD=60°,AB=4,AD=2,PB=
如图,在五面体P-ABCD中,底面ABCD是平行四边形,∠BAD=60°,AB=4,AD=2,PB=| 15 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
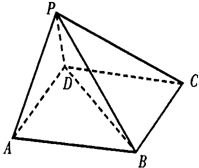 如图,在五面体P-ABCD中,底面ABCD是平行四边形,∠BAD=60°,AB=4,AD=2,PB=
如图,在五面体P-ABCD中,底面ABCD是平行四边形,∠BAD=60°,AB=4,AD=2,PB= ,PD=
,PD= .
.查看答案和解析>>
科目:高中数学 来源:2008-2009学年江西省吉安市白鹭洲中学高二(下)第一次月考数学试卷(解析版) 题型:解答题
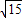 ,PD=
,PD=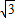 .
.
查看答案和解析>>
科目:高中数学 来源:2003-2004学年江苏省无锡市天一中学高二(下)期末数学试卷(普通班)(解析版) 题型:解答题
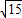 ,PD=
,PD=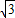 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com