
已知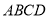 为直角梯形,
为直角梯形,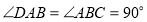 ,
,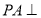 平面
平面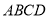 ,
,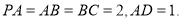
(1)求证: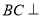 平面
平面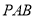 ;
;
(2)求平面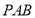 与平面
与平面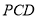 所成锐二面角的余弦值.
所成锐二面角的余弦值.
(1)详见解析;(2)锐二面角的余弦值为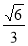 .
.
【解析】
试题分析:(1)证明法一可建立空间直角坐标系利用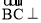 平面PAB的法向量即可
平面PAB的法向量即可
证明法二:要证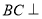 平面
平面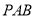 只要证BC⊥PA,而BC⊥PA由已知易得;
只要证BC⊥PA,而BC⊥PA由已知易得;
(2)先求平面PCD的法向量,再利用向量求二面角的公式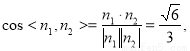 即可
即可
试题解析:
【解析】
如图,以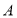 为原点建立空间直角坐标系,
为原点建立空间直角坐标系,
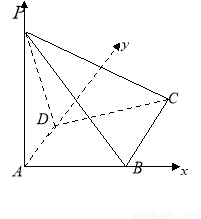
可得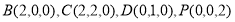 。2分
。2分
(1)证明法一:因为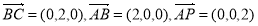 ,
,
所以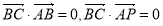 ,4分
,4分
所以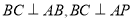 ,
,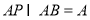 ,
,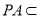 平面
平面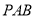 ,
,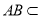 平面
平面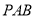 ,
,
所以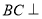 平面
平面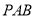 .6分
.6分
证明法二:因为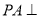 平面
平面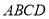 ,
,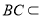 平面
平面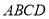 ,所以
,所以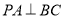 ,又因为
,又因为 =90°,即
=90°,即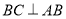 ,
,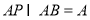 ,
,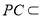 平面
平面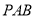 ,
,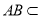 平面
平面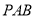 ,
,
所以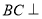 平面
平面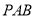 .6分
.6分
(2)由(1)知平面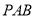 的一个法向量
的一个法向量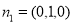 ,
,
设平面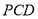 的法向量
的法向量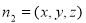 ,
,
又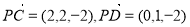 ,
,
且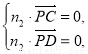
所以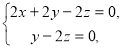
所以平面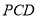 的一个法向量为
的一个法向量为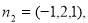
所以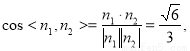
所以平面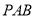 与平面
与平面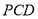 所成锐二面角的余弦值为
所成锐二面角的余弦值为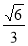 .12分
.12分
考点:1.线面垂直的证明;2.向量证明垂直问题;3.向量求二面角问题.


 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:高中数学 来源:2015届重庆市高二上学期期末考试理科数学试卷(解析版) 题型:选择题
抛掷一枚均匀的骰子(骰子的六个面上分别标有1、2、3、4、5、6个点)一次,观察掷出向上的点数,设事件A为掷出向上为偶数点,事件B为掷出向上为3点,则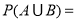 ( )
( )
A.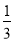 B.
B.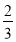 C.
C.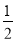 D.
D.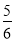
查看答案和解析>>
科目:高中数学 来源:2015届辽宁省沈阳市高二质量监测理科数学试卷(解析版) 题型:选择题
若等差数列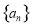 的前n项和为Sn,且S3=6,a1=4,则公差d等于 ( )
的前n项和为Sn,且S3=6,a1=4,则公差d等于 ( )
A.1 B.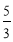 C.-2 D.3
C.-2 D.3
查看答案和解析>>
科目:高中数学 来源:2015届辽宁大连普通高中高二上学期期末考试理数学卷(解析版) 题型:选择题
下列命题中,真命题是( )
(A)?x0∈R,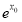 ≤0
≤0
(B)?x∈R,2x>x2
(C)双曲线 的离心率为
的离心率为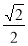
(D)双曲线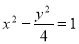 的渐近线方程为
的渐近线方程为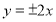
查看答案和解析>>
科目:高中数学 来源:2015届辽宁大连普通高中高二上学期期末考试文数学卷(解析版) 题型:选择题
直线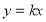 交双曲线
交双曲线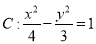 于
于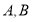 两点,
两点,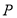 为双曲线
为双曲线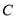 上异于
上异于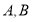 的任意一点,则直线
的任意一点,则直线 的斜率之积为( )
的斜率之积为( )
(A)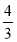 (B)
(B)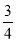 (C)
(C)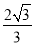 (D)
(D)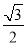
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com