
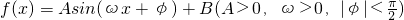 的图象上一个最高点的坐标为
的图象上一个最高点的坐标为 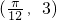 ,与之相邻的一个最低点的坐标为
,与之相邻的一个最低点的坐标为 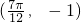 .
.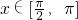 ,求函数f(x)的单调递增区间和零点.
,求函数f(x)的单调递增区间和零点. ,所以T=π,于是
,所以T=π,于是 (2分)
(2分) 解得
解得 (4分)
(4分)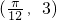 代入f(x)=2sin(2x+φ)+1,可得
代入f(x)=2sin(2x+φ)+1,可得 ,所以
,所以 ,
, ,因为
,因为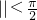 ,所以
,所以
 (7分)
(7分)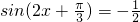 ,又∵
,又∵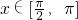
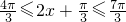 ∴
∴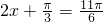 故
故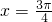 函数f(x)的零点是
函数f(x)的零点是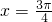 (10分)
(10分)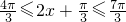 ∴由
∴由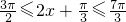 得
得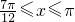 ∴函数f(x)的单调递增区间是
∴函数f(x)的单调递增区间是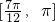 (13分)
(13分)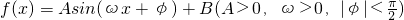 的图象上一个最高点的坐标为
的图象上一个最高点的坐标为 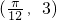 ,与之相邻的一个最低点的坐标为
,与之相邻的一个最低点的坐标为 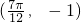 .我们可根据两个最值点的纵坐标求出A,B的值,根据横坐标求出周期T,进而得到ω及φ的值,从而求出求f(x)的表达式;
.我们可根据两个最值点的纵坐标求出A,B的值,根据横坐标求出周期T,进而得到ω及φ的值,从而求出求f(x)的表达式;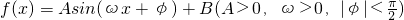 的解析式,是解答本题的关键.
的解析式,是解答本题的关键. 

科目:高中数学 来源:2009-2010学年广东省广州市培英中学高三(上)第一次月考数学试卷(理科)(解析版) 题型:解答题
 的图象上一个最高点的坐标为
的图象上一个最高点的坐标为 ,与之相邻的一个最低点的坐标为
,与之相邻的一个最低点的坐标为 .
. 处的切线方程.
处的切线方程.查看答案和解析>>
科目:高中数学 来源:2008年广东省佛山市高考数学二模试卷(理科)(解析版) 题型:解答题
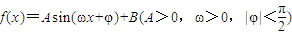 的图象上一个最高点的坐标为
的图象上一个最高点的坐标为 ,与之相邻的一个最低点的坐标为
,与之相邻的一个最低点的坐标为 .
. 处的切线方程.
处的切线方程.查看答案和解析>>
科目:高中数学 来源:2011年广东省湛江市遂溪县高考数学一模试卷(理科)(解析版) 题型:解答题
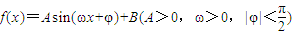 的图象上一个最高点的坐标为
的图象上一个最高点的坐标为 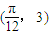 ,与之相邻的一个最低点的坐标为
,与之相邻的一个最低点的坐标为 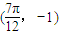 .
.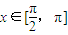 ,求函数f(x)的单调递增区间和零点.
,求函数f(x)的单调递增区间和零点.查看答案和解析>>
科目:高中数学 来源:2010年广东省高考数学冲刺预测试卷09(理科)(解析版) 题型:解答题
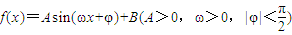 的图象上一个最高点的坐标为
的图象上一个最高点的坐标为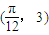 ,与之相邻的一个最低点的坐标为
,与之相邻的一个最低点的坐标为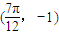 .
.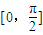 上的最大、最小值.
上的最大、最小值.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com