Question

甲乙两班进行消防安全知识竞赛，每班出3人组成甲乙两支代表队，首轮比赛每人一道必答题，答对则为本队得1分，答错不答都得0分，已知甲队3人每人答对的概率分别为，乙队每人答对的概率都是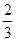．设每人回答正确与否相互之间没有影响，用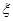表示甲队总得分．

（I）求随机变量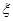的分布列及其数学期望E（）；

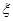（Ⅱ）求在甲队和乙队得分之和为4的条件下，甲队比乙队得分高的概率．

 

Answer 1

【答案】

（I）如下（Ⅱ）

【解析】

试题分析：解：（1）的可能取值为0，1，2，3

;;

;

的分布列为

	0	1	2	3

 

(2)设“甲队和乙队得分之和为4”为事件A,“甲队比乙队得分高”为事件B

则;

考点：分布列及其数学期望；概率

点评：求随机变量的分布列和数学期望是常考题型，解决这种题目关键是求出随机变量对应的概率。