Question

在1，2，3，…9这9个自然数中，任取3个不同的数．
（1）求这3个数中至少有1个是偶数的概率；
（2）求这3个数和为18的概率；
（3）设ξ为这3个数中两数相邻的组数（例如：若取出的数为1，2，3，则有两组相邻的数1，2和2，3，此时ξ的值是2）．求随机变量ξ的分布列及其数学期望Eξ．

Answer 1

解：（1）由题意知本题是一个等可能事件的概率，
试验发生所包含的事件数C₉³，
满足条件的事件3个数中至少有1个是偶数，包含三种情况一个偶数，两个偶数，三个偶数，
这三种情况是互斥的，根据等可能和互斥事件的概率公式得到
；
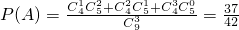
（2）记“这3个数之和为18”为事件B，
考虑三数由大到小排列后的中间数只有可能为5、6、7、8，
分别为459，567，468，369，279，378，189七种情况，
∴；
（3）随机变量ξ的取值为0，1，2，
P（ξ=0）=
P（ξ=1）=
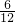
P（ξ=2）=
∴ξ的分布列为

∴ξ的数学期望为．
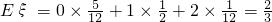
分析：（1）本题是一个等可能事件的概率，试验发生所包含的事件数C₉³，满足条件的事件3个数中至少有1个是偶数，包含三种情况一个偶数，两个偶数，三个偶数，写出每种情况的组合数，求出概率．
（2）本题是一个等可能事件的概率，试验发生所包含的事件数C₉³，，考虑三数由大到小排列后的中间数只有可能为5、6、7、8，分别为459，567，468，369，279，378，189七种情况，求出概率．
（3）ξ为这3个数中两数相邻的组数，随机变量ξ的取值为0，1，2，结合变量对应的事件写出变量的概率，写出分布列，利用期望公式做出期望值．
点评：本题考查离散型随机变量的分布列和期望，考查等可能事件的概率，是一个数字问题，这是一个比较典型的概率问题，注意做到不重不漏．
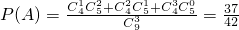
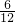
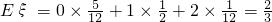