
【题目】已知点A(x1 , f(x1)),B(x2 , f(x2))是函数f(x)=2sin(ωx+φ) ![]() 图象上的任意两点,且角φ的终边经过点
图象上的任意两点,且角φ的终边经过点 ![]() ,若|f(x1)﹣f(x2)|=4时,|x1﹣x2|的最小值为
,若|f(x1)﹣f(x2)|=4时,|x1﹣x2|的最小值为 ![]() .
.
(1)求函数f(x)的解析式;
(2)求函数f(x)的单调递增区间;
(3)当 ![]() 时,不等式mf(x)+2m≥f(x)恒成立,求实数m的取值范围.
时,不等式mf(x)+2m≥f(x)恒成立,求实数m的取值范围.
【答案】
(1)解:角φ的终边经过点 ![]() ,
,
∴ ![]() ,
,
∵ ![]() ,∴
,∴ ![]() .
.
由|f(x1)﹣f(x2)|=4时,|x1﹣x2|的最小值为 ![]() ,得
,得 ![]() ,
,
即 ![]() ,∴ω=3
,∴ω=3
∴ ![]()
(2)解:由 ![]() ,
,
可得 ![]() ,
,
∴函数f(x)的单调递增区间为 ![]() k∈z
k∈z
(3)解:当 ![]() 时,
时, ![]() ,
,
于是,2+f(x)>0,
∴mf(x)+2m≥f(x)等价于 ![]()
由 ![]() ,得
,得 ![]() 的最大值为
的最大值为 ![]()
∴实数m的取值范围是 ![]() .
.
【解析】(1)利用三角函数的定义求出φ的值,由|f(x1)﹣f(x2)|=4时,|x1﹣x2|的最小值为 ![]() ,可得函数的周期,从而可求ω,进而可求函数f(x)的解析式;(2)利用正弦函数的单调增区间,可求函数f(x)的单调递增区间;(3)当
,可得函数的周期,从而可求ω,进而可求函数f(x)的解析式;(2)利用正弦函数的单调增区间,可求函数f(x)的单调递增区间;(3)当 ![]() 时,不等式mf(x)+2m≥f(x)恒成立,等价于
时,不等式mf(x)+2m≥f(x)恒成立,等价于 ![]() ,由此可求实数m的取值范围.
,由此可求实数m的取值范围.
【考点精析】掌握三角函数的最值是解答本题的根本,需要知道函数![]() ,当
,当![]() 时,取得最小值为
时,取得最小值为![]() ;当
;当![]() 时,取得最大值为
时,取得最大值为![]() ,则
,则![]() ,
,![]() ,
,![]() .
.


科目:高中数学 来源: 题型:
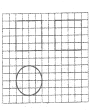
【题目】《九章算术》中,将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马,将四个面都为直角三角形的四面体称之为鳖臑,如图,网格纸上正方形小格的边长为![]() ,图中粗线画出的是某几何体毛坯的三视图,第一次切削,将该毛坯得到一个表面积最大的长方体,第二次切削沿长方体的对角面刨开,得到两个三棱柱,第三次切削将两个三棱柱分别沿棱和表面的对角线刨开得到两个鳖臑和两个阳马,则阳马与鳖臑的体积之比为( )
,图中粗线画出的是某几何体毛坯的三视图,第一次切削,将该毛坯得到一个表面积最大的长方体,第二次切削沿长方体的对角面刨开,得到两个三棱柱,第三次切削将两个三棱柱分别沿棱和表面的对角线刨开得到两个鳖臑和两个阳马,则阳马与鳖臑的体积之比为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,其中常数
,其中常数![]() .
.
(Ⅰ)当![]() ,求函数
,求函数![]() 的单调递增区间;
的单调递增区间;
(Ⅱ)设定义在![]() 上的函数
上的函数![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() , 若
, 若![]() 在
在![]() 内恒成立,则称
内恒成立,则称![]() 为函数
为函数![]() 的“类对称点”,当
的“类对称点”,当![]() 时,试问
时,试问![]() 是否存在“类对称点”,若存在,请求出一个“类对称点”的横坐标;若不存在,请说明理由.
是否存在“类对称点”,若存在,请求出一个“类对称点”的横坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中新网2016年12月19日电根据预报,今天开始雾霾范围将进一步扩大, ![]() 日夜间至
日夜间至![]() 日,雾霾严重时段部分地区
日,雾霾严重时段部分地区![]() 浓度峰值会超过
浓度峰值会超过![]() 微克/立方米. 而此轮雾霾最严重的时段,将有包括京津冀、山西、陕西、河南等
微克/立方米. 而此轮雾霾最严重的时段,将有包括京津冀、山西、陕西、河南等![]() 个省市在内的地区被雾霾笼罩.
个省市在内的地区被雾霾笼罩. ![]() 是指大气中直径小于或等于
是指大气中直径小于或等于![]() 微米的顆粒物,也称为可人肺颗粒物.
微米的顆粒物,也称为可人肺颗粒物. ![]() 日均值在
日均值在![]() 微克/立方米以下空气质量为一级;在
微克/立方米以下空气质量为一级;在![]() 微克/立方米
微克/立方米![]() 微克/立方米之间空气质量为二级;在
微克/立方米之间空气质量为二级;在![]() 微克/立方米以上空气质量为超标.某地区在2016年12月19日至28日每天的
微克/立方米以上空气质量为超标.某地区在2016年12月19日至28日每天的![]() 监测数据的茎叶图如下:
监测数据的茎叶图如下:

(1)求出这些数据的中位数与极差;
(2)从所给的空气质量不超标的![]() 天的数据中任意抽取
天的数据中任意抽取![]() 天的数据,求这
天的数据,求这![]() 天中恰好有
天中恰好有![]() 天空气质量为一级,另一天空气质量为二级的概率.
天空气质量为一级,另一天空气质量为二级的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△OAB的顶点坐标为O(0,0),A(2,9),B(6,﹣3),点P的横坐标为14,且 ![]() ,点Q是边AB上一点,且
,点Q是边AB上一点,且 ![]() .
.
(1)求实数λ的值与点P的坐标;
(2)求点Q的坐标;
(3)若R为线段OQ上的一个动点,试求 ![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出以下四个命题:
①若 ![]() <
< ![]() <0,则
<0,则 ![]() +
+ ![]() >2;
>2;
②若a>b,则am2>bm2;
③在△ABC中,若sinA=sinB,则A=B;
④任意x∈R,都有ax2﹣ax+1≥0,则0<a≤4.
其中是真命题的有( )
A.①②
B.②③
C.①③
D.③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() 的定义域是
的定义域是![]() ,对于以下四个命题:
,对于以下四个命题:
(1) 若![]() 是奇函数,则
是奇函数,则![]() 也是奇函数;
也是奇函数;
(2) 若![]() 是周期函数,则
是周期函数,则![]() 也是周期函数;
也是周期函数;
(3) 若![]() 是单调递减函数,则
是单调递减函数,则![]() 也是单调递减函数;
也是单调递减函数;
(4) 若函数![]() 存在反函数
存在反函数![]() ,且函数
,且函数![]() 有零点,则函数
有零点,则函数![]() 也有零点.
也有零点.
其中正确的命题共有
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数 ![]() 是定义在(﹣1,1)上的奇函数,且
是定义在(﹣1,1)上的奇函数,且 ![]() .
.
(1)确定函数的解析式;
(2)证明函数f(x)在(﹣1,1)上是增函数;
(3)解不等式f(t﹣1)+f(t)<0.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,曲线
,曲线![]() 在点
在点![]() 处的切线与直线
处的切线与直线![]() 垂直(其中
垂直(其中![]() 为自然对数的底数).
为自然对数的底数).
(I)求![]() 的解析式及单调递减区间;
的解析式及单调递减区间;
(II)是否存在常数![]() ,使得对于定义域内的任意
,使得对于定义域内的任意![]() 恒成立?若存在,求出
恒成立?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com