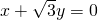练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    直线数学公式绕原点按顺时针方向旋转30°，所得直线与圆（x-2）2+y2=3的位置关系是


    1. A.
      相切
    2. B.
      相交但不过圆心
    3. C.
      相离
    4. D.
      相交且过圆心
    A
    分析：先求出所得直线方程，再计算 圆心到所得直线的距离，将此距离与圆的半径比较．
    解答：直线 斜率为-，倾斜角1500，绕原点按顺时针方向旋转30°后，
    得到的直线倾斜角1200，斜率为-，∴所得直线方程为：y=-x，即 x+y=0，
    圆心到所得直线的距离为：==半径 ，
    所得直线与圆（x-2）2+y2=3的位置关系是相切．
    故选A．
    点评：本题考查直线和圆的位置关系．直线方程的求法，考查计算能力．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2011-2012学年安徽省蚌埠四校联盟高一自主招生考试数学试卷（解析版） 题型：填空题

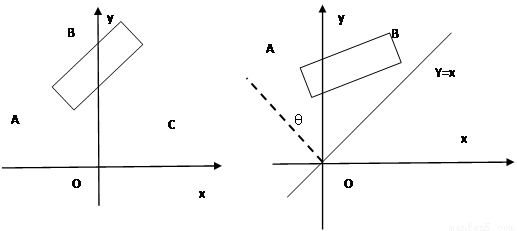
    如图1，在平面直角坐标系中，边长为1的正方形OABC的顶点B在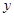轴的正半轴上，O为坐标原点.现将正方形OABC绕O点按顺时针方向旋转.

    　(1)当点A第一次落到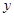轴正半轴上时，求边BC在旋转过程中所扫过的面积；

    　（2）若线段AB与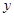轴的交点为M（如图2）,线段BC与直线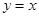的交点为N.设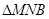的周长为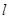,在正方形OABC旋转的过程中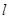值是否有改变？并说明你的结论；

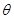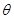    (3)设旋转角为，当为何值时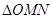，的面积最小？求出这个最小值， 并求出此时△BMN的内切圆半径.

          

     

    查看答案和解析>>

    同步练习册答案