已知α为第二象限角，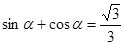
，则cos2α=（ ）
A． | B． | C． | D． |
A
解析试题分析：由α为第二象限角，可知sinα＞0，cosα＜0，从而可求得sinα-cosα的值，利用cos2α=-（sinα-cosα）（sinα+cosα）可求得cos2α．解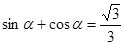：∵，两边平方得：1+sin2α=
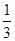，∴sin2α=-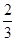
，①∴（sinα-cosα）2=1-sin2α=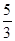
∵α为第二象限角，∴sinα＞0，cosα＜0，∴sinα-cosα=
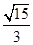，②∴cos2α=-（sinα-cosα）（sinα+cosα）=（-）×
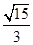=-．故答案为：A．
考点：同角三角函数，二倍角的正弦
点评：本题考查同角三角函数间的基本关系，突出二倍角的正弦与余弦的应用，求得sinα-cosα的值是关键，属于中档题．
阅读快车系列答案科目：高中数学 来源： 题型：单选题
设k∈Z，函数y=sin(
)sin(
)的单调递增区间为( )
| A．[(2k+1)π,2(k+1)π] | B．[(k+ )π,(k+1)π] |
| C．[kπ,(k+) π] | D．[2kπ, (2k+1)π] |
查看答案和解析>>
科目：高中数学 来源： 题型：单选题
关于函数
的四个结论：
P1：函数
的最大值为
；
P2：把函数
的图象向右平移
个单位后可得到函数的图象；
P3：函数的单调递增区间为[
]，
；
P4：函数图象的对称中心为(
)，．其中正确的结论有（ ）
| A．1个 | B．2个 | C．3个 | D．4个 |
查看答案和解析>>
科目：高中数学 来源： 题型：单选题
已知函数f(x)=sinwx+coswx(w>0)，如果存在实数x1，使得对任意的实数x，都有
成立，则w的最小值为( )
A． | B． | C． | D． |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
的一部分，则其解析表达式为（ ）
＝( )
，
，则
（ ）
，且
的终边上一点的坐标为
，则
