
【题目】已知函数f(x)=x2+2cosx,g(x)=ex(cosx﹣sinx+2x﹣2),其中e≈2.17828…是自然对数的底数.(13分)
(Ⅰ)求曲线y=f(x)在点(π,f(π))处的切线方程;
(Ⅱ)令h(x)=g (x)﹣a f(x)(a∈R),讨论h(x)的单调性并判断有无极值,有极值时求出极值.
【答案】解:(Ⅰ)f(π)=π2﹣2.f′(x)=2x﹣2sinx,∴f′(π)=2π.
∴曲线y=f(x)在点(π,f(π))处的切线方程为:y﹣(π2﹣2)=2π(x﹣π).
化为:2πx﹣y﹣π2﹣2=0.
(Ⅱ)h(x)=g (x)﹣a f(x)=ex(cosx﹣sinx+2x﹣2)﹣a(x2+2cosx)
h′(x)=ex(cosx﹣sinx+2x﹣2)+ex(﹣sinx﹣cosx+2)﹣a(2x﹣2sinx)
=2(x﹣sinx)(ex﹣a)=2(x﹣sinx)(ex﹣elna).
令u(x)=x﹣sinx,则u′(x)=1﹣cosx≥0,∴函数u(x)在R上单调递增.
∵u(0)=0,∴x>0时,u(x)>0;x<0时,u(x)<0.
(i)a≤0时,ex﹣a>0,∴x>0时,h′(x)>0,函数h(x)在(0,+∞)单调递增;
x<0时,h′(x)<0,函数h(x)在(﹣∞,0)单调递减.
∴x=0时,函数h(x)取得极小值,h(0)=﹣1﹣2a.
(ii)a>0时,令h′(x)=2(x﹣sinx)(ex﹣elna)=0.
解得x1=lna,x2=0.
①0<a<1时,x∈(﹣∞,lna)时,ex﹣elna<0,h′(x)>0,函数h(x)单调递增;
x∈(lna,0)时,ex﹣elna>0,h′(x)<0,函数h(x)单调递减;
x∈(0,+∞)时,ex﹣elna>0,h′(x)>0,函数h(x)单调递增.
∴当x=0时,函数h(x)取得极小值,h(0)=﹣2a﹣1.
当x=lna时,函数h(x)取得极大值,h(lna)=﹣a[ln2a﹣2lna+sin(lna)+cos(lna)+2].
②当a=1时,lna=0,x∈R时,h′(x)≥0,∴函数h(x)在R上单调递增.
③1<a时,lna>0,x∈(﹣∞,0)时,ex﹣elna<0,h′(x)>0,函数h(x)单调递增;
x∈(0,lna)时,ex﹣elna<0,h′(x)<0,函数h(x)单调递减;
x∈(lna,+∞)时,ex﹣elna>0,h′(x)>0,函数h(x)单调递增.
∴当x=0时,函数h(x)取得极大值,h(0)=﹣2a﹣1.
当x=lna时,函数h(x)取得极小值,h(lna)=﹣a[ln2a﹣2lna+sin(lna)+cos(lna)+2].
综上所述:a≤0时,函数h(x)在(0,+∞)单调递增;x<0时,函数h(x)在(﹣∞,0)单调递减.
x=0时,函数h(x)取得极小值,h(0)=﹣1﹣2a.
0<a<1时,函数h(x)在x∈(﹣∞,lna)是单调递增;函数h(x)在x∈(lna,0)上单调递减.当x=0时,函数h(x)取得极小值,h(0)=﹣2a﹣1.当x=lna时,函数h(x)取得极大值,h(lna)=﹣a[ln2a﹣2lna+sin(lna)+cos(lna)+2].
当a=1时,lna=0,函数h(x)在R上单调递增.
a>1时,函数h(x)在(﹣∞,0),(lna,+∞)上单调递增;函数h(x)在(0,lna)上单调递减.当x=0时,函数h(x)取得极大值,h(0)=﹣2a﹣1.当x=lna时,函数h(x)取得极小值,h(lna)=﹣a[ln2a﹣2lna+sin(lna)+cos(lna)+2].
【解析】(Ⅰ)f(π)=π2﹣2.f′(x)=2x﹣2sinx,可得f′(π)=2π即为切线的斜率,利用点斜式即可得出切线方程.
(Ⅱ)h(x)=g (x)﹣a f(x)=ex(cosx﹣sinx+2x﹣2)﹣a(x2+2cosx),可得h′(x)=2(x﹣sinx)(ex﹣a)=2(x﹣sinx)(ex﹣elna).令u(x)=x﹣sinx,则u′(x)=1﹣cosx≥0,可得函数u(x)在R上单调递增.
由u(0)=0,可得x>0时,u(x)>0;x<0时,u(x)<0.
对a分类讨论:a≤0时,0<a<1时,当a=1时,a>1时,利用导数研究函数的单调性极值即可得出.
【考点精析】解答此题的关键在于理解导数的加减法法则的相关知识,掌握导数加减法法则:![]() ,以及对导数的乘除法法则的理解,了解导数的乘除法法则:
,以及对导数的乘除法法则的理解,了解导数的乘除法法则:![]() ;
;![]() .
.


科目:高中数学 来源: 题型:
【题目】已知{xn}是各项均为正数的等比数列,且x1+x2=3,x3﹣x2=2.(12分)
(Ⅰ)求数列{xn}的通项公式;
(Ⅱ)如图,在平面直角坐标系xOy中,依次连接点P1(x1 , 1),P2(x2 , 2)…Pn+1(xn+1 , n+1)得到折线P1 P2…Pn+1 , 求由该折线与直线y=0,x=x1 , x=xn+1所围成的区域的面积Tn . 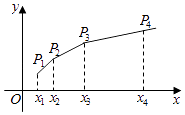
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() ,
,![]() .
.
(1)直线![]() 是否过定点?若过定点,求出该定点坐标,若不过定点,请说明理由;
是否过定点?若过定点,求出该定点坐标,若不过定点,请说明理由;
(2)已知点![]() ,若直线
,若直线![]() 上存在点
上存在点![]() 满足条件
满足条件![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】△ABC的内角A,B,C的对边分别为a,b,c,已知△ABC的面积为 ![]() .(12分)
.(12分)
(1)求sinBsinC;
(2)若6cosBcosC=1,a=3,求△ABC的周长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某班主任从本班![]() 名男生,
名男生,![]() 名女生中随机抽取一个容量为
名女生中随机抽取一个容量为![]() 的样本,对他们的数学及物理成绩进行分析,这
的样本,对他们的数学及物理成绩进行分析,这![]() 名同学的数学及物理成绩(单位:分数)对应如下表:
名同学的数学及物理成绩(单位:分数)对应如下表:
学生序号 |
|
|
|
|
|
|
|
数学成绩 |
|
|
|
|
|
|
|
物理成绩 |
|
|
|
|
|
|
|
(1)根据以上数据,求物理成绩![]() 关于数学成绩
关于数学成绩![]() 的线性回归方程(系数均精确到
的线性回归方程(系数均精确到![]() ),并预测班上某位数学成绩为
),并预测班上某位数学成绩为![]() 分的同学的物理成绩(保留到整数);
分的同学的物理成绩(保留到整数);
(2)从物理成绩不低于![]() 分的样本学生中随机抽取
分的样本学生中随机抽取![]() 人,求抽到的
人,求抽到的![]() 人数学成绩也不低于
人数学成绩也不低于![]() 分的概率.
分的概率.
参考公式:
已经计算出:![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
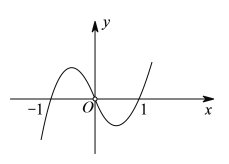
【题目】已知函数![]() 的图象如图所示(其中
的图象如图所示(其中![]() 是定义域为
是定义域为![]() 的函数
的函数![]() 的导函数),则以下说法错误的是( ).
的导函数),则以下说法错误的是( ).
A. ![]()
B. 当![]() 时,函数
时,函数![]() 取得极大值
取得极大值
C. 方程![]() 与
与![]() 均有三个实数根
均有三个实数根
D. 当![]() 时,函数
时,函数![]() 取得极小值
取得极小值
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com