
在棱长为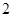 的正方体
的正方体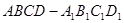 中,
中,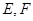 分别为
分别为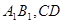 的中点.
的中点.
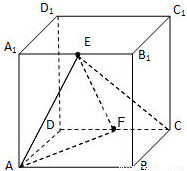
(1)求直线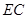 与平面
与平面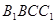 所 成 角的大小;
所 成 角的大小;
(2)求二面角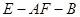 的大小.
的大小.
(1) 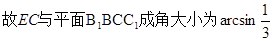 (2)
(2) 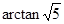
【解析】
试题分析:(1)解法一:建立坐标系
平面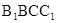 的一个法向量为
的一个法向量为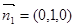
因为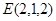
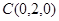 ,
,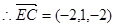 ,
,
可知直线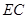 的一个方向向量为
的一个方向向量为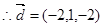 .
.
设直线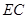 与平面
与平面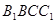 成角为
成角为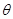 ,
,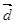 与
与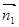 所成角为
所成角为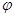 ,则
,则
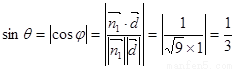
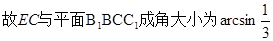
解法二: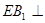 平面
平面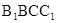 ,即
,即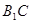 为
为 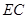 在平面
在平面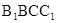 内的射影,
内的射影,
故 为直线
为直线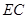 与平面
与平面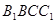 所成角,
所成角,
在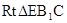 中,
中,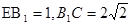 ,
,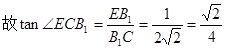
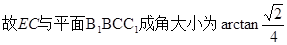
(2)解法一:建立坐标系如图.平面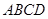 的一个法向量为
的一个法向量为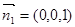
设平面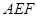 的一个法向量为
的一个法向量为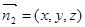 ,因为
,因为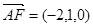 ,
,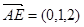
所以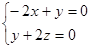 ,令
,令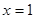 ,则
,则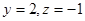
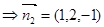
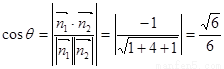
由图知二面角 为锐二面角,故其大小为
为锐二面角,故其大小为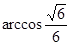 .
.
解法二:过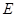 作平面
作平面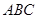 的垂线,垂足为
的垂线,垂足为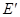 ,
,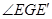 即为所求
即为所求
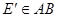 ,过
,过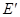 作
作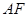 的垂线设垂足为
的垂线设垂足为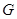 ,
,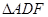 ∽
∽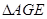
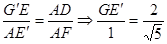 即
即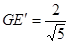 在
在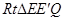 中
中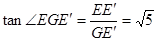
所以 二面角 的大小为
的大小为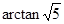 .
.
考点:空间中角的求解
点评:解决的关键是利用角的定义作图来结合几何中的性质定理和判定定理来得到,解三角形得到,或者建立空间直角坐标系,运用向量法来求解。属于中档题。


科目:高中数学 来源:2014届山东省济宁市高二5月质量检测理科数学试卷(解析版) 题型:选择题
在棱长为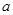 的正方体
的正方体 中,错误的是( )
中,错误的是( )

A.直线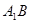 和直线
和直线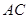 所成角的大小为
所成角的大小为
B.直线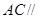 平面
平面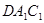
C.二面角 的大小是
的大小是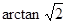
D.直线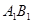 到平面
到平面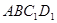 的距离为
的距离为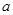
查看答案和解析>>
科目:高中数学 来源:2012年人教A版高中数学选修2-1 3.2立体几何中的向量方法练习卷(解析版) 题型:选择题
在棱长为 的正方体
的正方体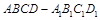 中,则平面
中,则平面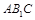 与平面
与平面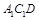 间的距离 ( )
间的距离 ( )
A.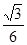 B.
B.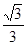 C
.
C
.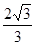 D.
D.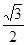
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com