Question

在xOy坐标平面内，已知圆C过点A（1，1）和点B（1，5），且圆心C在直线2x+y-2=0上．
（1）求圆C的方程；
（2）求过点A且与圆C相切的直线方程；
（3）已知斜率为-1的直线l与圆C相交于P，Q两点，且CP⊥CQ，试求直线l的方程．

Answer 1

解：（1）由题意，设圆心坐标为C（a，b），则
∵圆C过点A（1，1）和点B（1，5），
∴（a-1）²+（b-1）²=（a-1）²+（b-5）²
∴b=3
又圆心C在直线2x+y-2=0上．
∴2a+b-2=0，∴
∴圆C的方程 ；
（2）
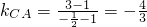
∴相切的直线方程斜率为
∴相切的直线方程为3x-4y+1=0
（3）设斜率为-1的直线l的方程为y=-x+b，代入圆的方程，化简得2x²+（7-2b）x+b²+3=0
设P（x₁，y₁），Q（x₂，y₂），则
∴2b²-5b=0
∴
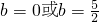
∴所求方程为y=-x或，
经检验，符合题意．
分析：（1）求圆C的方程，关键是确定圆心的坐标及圆的半径，根据圆心C在直线2x+y-2=0上，可确定圆心坐标，从而可解；
（2）先求CA斜率，再求切线方程；
（3）假设直线方程与圆方程联立，利用CP⊥CQ，用向量的数量积为0，可求直线l的方程．
点评：本题以圆为载体，考查直线与圆的位置关系，考查圆的标准方程，圆的切线方程，考查向量垂直条件的运用．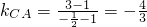
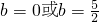