
 如图,三定点
如图,三定点![]() 三动点D、E、M满足
三动点D、E、M满足
![]()
![]()
(I)求动直线DE斜率的变化范围;
(II)求动点M的轨迹方程。
解法一:如图(Ⅰ)设 D(xD,yD), E (xC,yC) , M (x,y).
由 ![]() ,知(xD-2,yD-1)=t(-2,-2).
,知(xD-2,yD-1)=t(-2,-2).
∴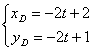
![]() 同理
同理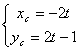
∴![]()
∵t∈[0,1], ∴kDC∈[-1,1].
(Ⅱ)∵![]() .
.
∴(x+2t-2,y+2t-1)=t(-2t+2t-2,2t-1+2t-1)
=t(-2,4t-2)=(-2t,4t2-2t).
∴![]() ∴
∴![]() ,即x2=4y.
,即x2=4y.
∵t∈[0,1],
∴x=2(1-2t)∈[-2,2].
即所求轨迹方程为 x2=4y , x∈[-2,2].
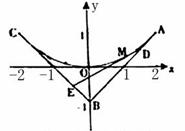
解法二:(Ⅰ)同上.
(Ⅱ)如图,
![]() ,
,
![]()
![]()
![]()
设M点坐标为(x,y),由![]() 得
得
=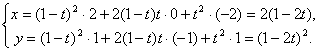 消去t得 x2=4y.
消去t得 x2=4y.
∵t∈[0,1],∴x∈[-2,2]. 故轨迹方程是 x2=4y, x∈[-2,2].


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:高中数学 来源: 题型:
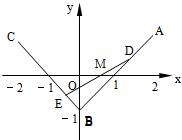 如图,三定点A(2,1),B(0,-1),C(-2,1);三动点D,E,M满足
如图,三定点A(2,1),B(0,-1),C(-2,1);三动点D,E,M满足| AD |
| AB |
| BE |
| BC |
| DM |
| DE |
查看答案和解析>>
科目:高中数学 来源:新人教版2012届高三上学期单元测试(6)数学试题 人教版 题型:044
(文)如图,三定点A(2,1),B(0,-1),C(-2,1);三动点D,E,M满足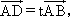
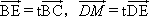 ,t∈[0,1].
,t∈[0,1].
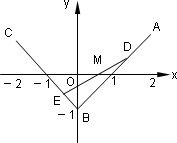
(Ⅰ)求动直线DE斜率的变化范围;(Ⅱ)求动点M的轨迹方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com