
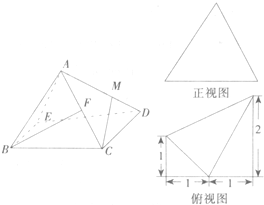
 (2012•石家庄一模)四棱锥的正视图和俯视图如图,其中俯视图是直角梯形.
(2012•石家庄一模)四棱锥的正视图和俯视图如图,其中俯视图是直角梯形.| BF |
| CM |
| 3 |
| AD |
| p |
| ||
| 4 |
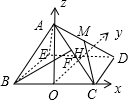 解:(I )若正视图是等边三角形,F为AC的中点,当点M在棱AD上移动时,总有BF丄CM.
解:(I )若正视图是等边三角形,F为AC的中点,当点M在棱AD上移动时,总有BF丄CM.| 3 |
| 1 |
| 2 |
| ||
| 2 |
| 3 |
| BF |
| 3 |
| 2 |
| ||
| 2 |
| CM |
| 3 |
| BF |
| CM |
| ED |
| AD |
| m |
| m |
| ED |
| m |
| AD |
|
| m |
| 3 |
| a |
| n |
| m |
| n |
| -2 | ||||
|
| -2 | ||||
|
| ||
| 2 |
| 3 |
| p |
| BA |
| 3 |
| BE |
| p |
| BA |
| p |
| BE |
|
| p |
| 3 |
| AD |
| p |
| ||
| 4 |
| ||
| 4 |


 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com