
 小题满分12分)在直三棱柱
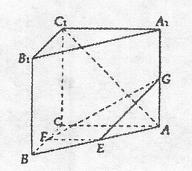
小题满分12分)在直三棱柱 ABC—A1B1C1中,CA=CB=CC1=2,
ABC—A1B1C1中,CA=CB=CC1=2, ,E、F分别是BA、BC的中点,G是AA1上一点,且
,E、F分别是BA、BC的中点,G是AA1上一点,且
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案科目:高中数学 来源:不详 题型:解答题
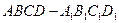 中,以正方体的三条棱所在直线为轴建立空间直角坐标系
中,以正方体的三条棱所在直线为轴建立空间直角坐标系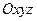 ,
,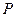 在线段
在线段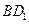 上,且满足
上,且满足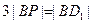 ,试写出点
,试写出点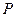 的坐标并写出
的坐标并写出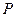 关于平面
关于平面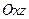 的对称点
的对称点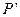 的坐标;
的坐标;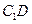 中点为
中点为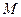 ,求点
,求点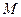 到点
到点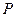 的距离。
的距离。查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
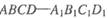 中,直线
中,直线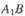 与平面
与平面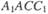 所成的角为
所成的角为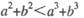 (B)
(B)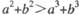
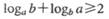 (D)
(D)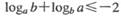
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 内的一条直线,P为
内的一条直线,P为 外一点,PA=2,P到
外一点,PA=2,P到 的距离是1,记AC与PA所成的角为
的距离是1,记AC与PA所成的角为 ,则必有( )
,则必有( )A. | B.cos ≤ ≤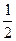 | C.sin ≥ ≥ | D.tan ≥ ≥ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com