
 经过
经过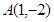 ,
, 两点,且在两坐标轴上的四个截距之和为2.
两点,且在两坐标轴上的四个截距之和为2. 的方程;
的方程;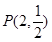 为圆内一点,求经过点
为圆内一点,求经过点 被圆
被圆 截得的弦长最短时的直线
截得的弦长最短时的直线 的方程.
的方程. ;(2)
;(2) .
. ,再令
,再令 、
、 ,分别求出圆在
,分别求出圆在 轴、
轴、 轴上的截距之和,再有已知圆两坐标轴上的四个截距之和为2.得出
轴上的截距之和,再有已知圆两坐标轴上的四个截距之和为2.得出 的关系式,由于
的关系式,由于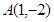 ,
, 两点在圆上,联立方程组,解方程组求出系数
两点在圆上,联立方程组,解方程组求出系数 ,从而求得圆的方程;(2)考查圆的最短弦,实际上当直线
,从而求得圆的方程;(2)考查圆的最短弦,实际上当直线 过定点
过定点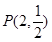 且与过此点的圆的半径垂直时,
且与过此点的圆的半径垂直时, 被圆截得的弦长最短,求出直线
被圆截得的弦长最短,求出直线 的斜率,再由直线方程的点斜式求出方程.
的斜率,再由直线方程的点斜式求出方程. 的方程为
的方程为 ,
, ,得
,得 ,则圆在
,则圆在 轴上的截距之和为
轴上的截距之和为 ;
; ,得
,得 ,则圆在
,则圆在 轴上的截距之和为
轴上的截距之和为 ;
; ,即
,即 ,又
,又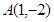 ,
, 两点在圆上,
两点在圆上, ,解得
,解得 ,故所求圆
,故所求圆 的方程为
的方程为 .
. 的方程为
的方程为 ,圆心为
,圆心为 ,
, 过定点
过定点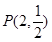 且与过此点的圆的半径垂直时,
且与过此点的圆的半径垂直时, 被圆截得的弦长最短,
被圆截得的弦长最短, ,
,
 ,
, 的方程为
的方程为 ,即
,即 .
.

 53天天练系列答案
53天天练系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com