△ABC的三个顶点为A(-3,0),B(2,1),C(-2,3),求:
(1)BC所在直线的方程;
(2)BC边上中线AD所在直线的方程;
(3)BC边上的垂直平分线DE的方程.
解:(1)因为直线BC经过B(2,1)和C(-2,3)两点,由两点式得BC的方程为y-1=
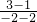
(x-2),即x+2y-4=0.
(2)设BC中点D的坐标为(x,y),则x=
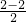
=0,y=
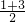
=2.
BC边的中线AD过点A(-3,0),D(0,2)两点,由截距式得AD所在直线方程为
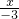
+

=1,即2x-3y+6=0.
(3)BC的斜率k
1=-

,则BC的垂直平分线DE的斜率k
2=2,由斜截式得直线DE的方程为y=2x+2.
分析:(1)利用B和C的坐标直接求出直线方程即可;(2)根据中点坐标公式求出B与C的中点D的坐标,利用A和D的坐标写出中线方程即可;(3)求出直线BC的斜率,然后根据两直线垂直时斜率乘积为-1求出BC垂直平分线的斜率,由(2)中D的坐标,写出直线DE的方程即可.
点评:考查学生会根据一点和斜率或两点坐标写出直线的方程,掌握两直线垂直时斜率的关系.会利用中点坐标公式求线段的中点坐标.

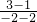 (x-2),即x+2y-4=0.
(x-2),即x+2y-4=0.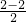 =0,y=
=0,y=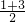 =2.
=2.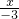 +
+ =1,即2x-3y+6=0.
=1,即2x-3y+6=0. ,则BC的垂直平分线DE的斜率k2=2,由斜截式得直线DE的方程为y=2x+2.
,则BC的垂直平分线DE的斜率k2=2,由斜截式得直线DE的方程为y=2x+2.
