
已知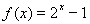 ,
, ,规定:当
,规定:当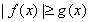 时,
时, 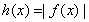 ;当
;当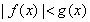 时,
时,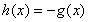 ,则
,则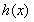 ( )
( )
A.有最小值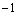 ,最大值1 B.有最大值1,无最小值
,最大值1 B.有最大值1,无最小值
C.有最小值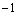 ,无最大值 D.有最大值
,无最大值 D.有最大值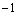 ,无最小值
,无最小值
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案科目:高中数学 来源: 题型:
如图,已知圆![]() 与
与![]() 轴负半轴的交点为
轴负半轴的交点为![]() . 由点
. 由点![]() 出发的射线
出发的射线![]() 的斜率为
的斜率为![]() . 射线
. 射线![]() 与圆
与圆![]() 相交于另一点
相交于另一点![]()

(1)当![]() 时,试用
时,试用![]() 表示点
表示点![]() 的坐标;
的坐标;
(2)当![]() 时,求证:“射线
时,求证:“射线![]() 的斜率
的斜率![]() 为有理数”是“点
为有理数”是“点![]() 为单位圆
为单位圆![]() 上的有理点”的充要条件;(说明:坐标平面上,横、纵坐标都为有理数的点为有理点.我们知道,一个有理数可以表示为
上的有理点”的充要条件;(说明:坐标平面上,横、纵坐标都为有理数的点为有理点.我们知道,一个有理数可以表示为![]() ,其中
,其中![]() 、
、![]() 均为整数且
均为整数且![]() 、
、![]() 互质)
互质)
(3)定义:实半轴长![]() 、虚半轴长
、虚半轴长![]() 和半焦距
和半焦距![]() 都是正整数的双曲线为“整勾股双曲线”.
都是正整数的双曲线为“整勾股双曲线”.
当![]() 为有理数且
为有理数且![]() 时,试证明:一定能构造偶数个“整勾股双曲线”(规定:实轴长和虚轴长都对应相等的双曲线为同一个双曲线),它的实半轴长、虚半轴长和半焦距的长恰可由点
时,试证明:一定能构造偶数个“整勾股双曲线”(规定:实轴长和虚轴长都对应相等的双曲线为同一个双曲线),它的实半轴长、虚半轴长和半焦距的长恰可由点![]() 的横坐标、纵坐标和半径
的横坐标、纵坐标和半径![]() 的数值构成. 说明你的理由并请尝试给出构造方法.
的数值构成. 说明你的理由并请尝试给出构造方法.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年湖南省、岳阳县一中高三11月联考文科数学 题型:填空题
已知集合 为非空集合,且
为非空集合,且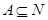 ,定义
,定义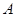 的“交替和”如下:将集合
的“交替和”如下:将集合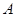 中的元素按由大到小排列,然后从最大的数开始,交替地减、加后续的数,直到最后一个数,并规定单元素集合的交替和为该元素。例如集合
中的元素按由大到小排列,然后从最大的数开始,交替地减、加后续的数,直到最后一个数,并规定单元素集合的交替和为该元素。例如集合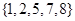 的交替和为8-7+5-2+1=5,集合
的交替和为8-7+5-2+1=5,集合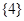 的交替和为4,当
的交替和为4,当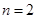 时,集合
时,集合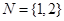 的非空子集为
的非空子集为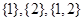 ,记三个集合的交替和的总和为
,记三个集合的交替和的总和为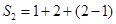 = 4,则
= 4,则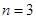 时,集合
时,集合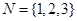 的所有非空子集的交替和的总和
的所有非空子集的交替和的总和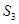 =
;集合
=
;集合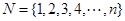 的所有非空子集的交替和的总和
的所有非空子集的交替和的总和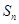 =
=
查看答案和解析>>
科目:高中数学 来源:2010-2011学年福建省高三上学期期末考试数学文卷 题型:解答题
(14分)已知函数 ,
,
(Ⅰ)若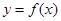 在[-1,1]上存在零点,求实数
在[-1,1]上存在零点,求实数 的取值范围;
的取值范围;
(Ⅱ)当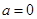 时,若对任意的
时,若对任意的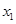 ∈[1,4],总存在
∈[1,4],总存在 ∈[1,4],使
∈[1,4],使 成立,求实数
成立,求实数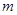 的取值范围;
的取值范围;
(Ⅲ)若函数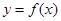 (其中
(其中 )的值域为区间D,是否存在常数
)的值域为区间D,是否存在常数 ,使区间D的长度为
,使区间D的长度为 ?若存在,求出
?若存在,求出 的值;若不存在,请说明理由。(规定:区间
的值;若不存在,请说明理由。(规定:区间 的长度为
的长度为 ).
).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com