
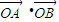 ,再代入向量的夹角公式,求出∠AOB的余弦值,再判断正负即可.
,再代入向量的夹角公式,求出∠AOB的余弦值,再判断正负即可.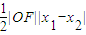 ,再把(I)中求出的x1x2,x1+x2的值代入,就可用含k的式子表示S△ABO,再求最值即可.
,再把(I)中求出的x1x2,x1+x2的值代入,就可用含k的式子表示S△ABO,再求最值即可.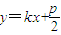
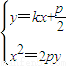 ,得x2-2pkx-p2=0
,得x2-2pkx-p2=0
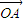 •
•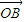 =
=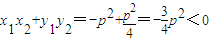

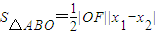 =
=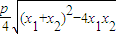 =
=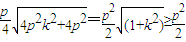 当k=0时取等号
当k=0时取等号
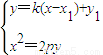 得
得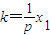
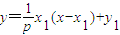 令x=0,得
令x=0,得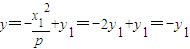


科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:崇文区一模 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2006年北京市崇文区高考数学一模试卷(理科)(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com