
平面上有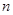 条直线, 这
条直线, 这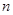 条直线任意两条不平行, 任意三条不共点, 记这
条直线任意两条不平行, 任意三条不共点, 记这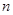 条直线将平面分成
条直线将平面分成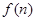 部分, 则
部分, 则 ___________,
___________,
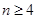 时,
时,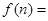 _________________.)(用
_________________.)(用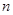 表示).
表示).
 ,
,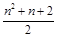
【解析】
试题分析:根据一条直线可以把平面分成两部分,两条直线最多可以把平面分成4部分,三条直线最多可以把平面分成7部分,四条直线最多可以把平面分成11部分,找出规律即可解:两条直线可以把平面分成4部分, 3条直线(直线相互不平行也不通过同一个点)把平面分成7部分,作第4条直线,它与前3条直线交于3点,这3点把第4条直线分成4段,相应地平面也就增加了4部分,4条直线把平面分成7+4=11部分,作第5条直线,它被分成5段,相应地平面增加5部分,所以5条直线把平面分成7+4+5=16部分,于是6条直线把平面分成7+4+5+6=22部分,事实上,1条直线把平面分成2部分,2条直线把平面分成2+2=4部分,3条直线把平面分成2+2+3=7部分,那么n条直线把平面分成2+2+3+4+…+n=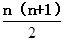 +1部分.故答案为:7,
+1部分.故答案为:7,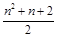 .
.
考点:归纳推理
点评:本题考查了在平面中直线相交于产生平面数量的关系,关键找规律,难度较大.


 发散思维新课堂系列答案
发散思维新课堂系列答案科目:高中数学 来源: 题型:
| 1 | 3 |
查看答案和解析>>
科目:高中数学 来源:2012-2013学年广东省韶关市高三第一次调研测试数学理科试卷(解析版) 题型:填空题
平面上有 条直线, 这
条直线, 这 条直线任意两条不平行, 任意三条不共点, 记这
条直线任意两条不平行, 任意三条不共点, 记这 条直线将平面分成
条直线将平面分成 部分, 则
部分, 则 ___________,
___________,
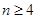 时,
时,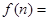 _________________.)(用
_________________.)(用 表示).
表示).
查看答案和解析>>
科目:高中数学 来源: 题型:
①如果一个平面经过一条直线,那么这条直线上的所有点都在这个平面之内 ②直线a![]() 平面α
平面α![]() a上的两个点在α内 ③如果直线a上有一个点不在α内,那么直线a不在α内
a上的两个点在α内 ③如果直线a上有一个点不在α内,那么直线a不在α内
A.0 B
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com