
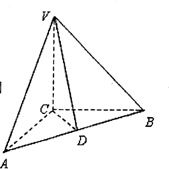
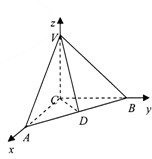
 如图,△VAC中,VC⊥AC,将其绕直线VC旋转得到△VBC,D是AB的中点,AB=
如图,△VAC中,VC⊥AC,将其绕直线VC旋转得到△VBC,D是AB的中点,AB=| 2 |
| π |
| 2 |
| n |
| n |
| 2 |
| π |
| 2 |
| 2 |
| a |
| 2 |
| a |
| 2 |
| ||
| 2 |
| VD |
| a |
| 2 |
| a |
| 2 |
| ||
| 2 |
| CD |
| a |
| 2 |
| a |
| 2 |
| AB |
| AB |
| CD |
| AB |
| VD |
| n |
| n |
| AB |
| n |
| VD |
|
| n |
| ||
| tanθ |
| BC |
| ||||
|
|
| ||
| 2 |
| π |
| 2 |
| ||
| 2 |
| π |
| 2 |
| π |
| 4 |


 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案科目:高中数学 来源: 题型:
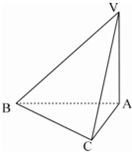 如图,已知三棱锥V-ABC中,∠VAB=∠VAC=∠ABC=90°且BC=1,AC=2,VA=2.
如图,已知三棱锥V-ABC中,∠VAB=∠VAC=∠ABC=90°且BC=1,AC=2,VA=2.查看答案和解析>>
科目:高中数学 来源:2002年高中会考数学必备一本全2002年1月第1版 题型:044
如图,在三棱锥V-ABC中,已知∠VAB=∠VAC=∠ABC= ,且BC=a,AB=b,AV=c,求:
,且BC=a,AB=b,AV=c,求:

(1)二面角A-VB-C的平面角的度数;
(2)BV与CA夹角的余弦值.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年湖南省郴州市汝城县高一(上)第二次单元检测数学试卷(解析版) 题型:解答题
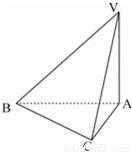 如图,已知三棱锥V-ABC中,∠VAB=∠VAC=∠ABC=90°且BC=1,AC=2,VA=2.
如图,已知三棱锥V-ABC中,∠VAB=∠VAC=∠ABC=90°且BC=1,AC=2,VA=2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com