解:(1)定义在R上的函数f(x)满足对任意实数m,n,总有f(m+n)=f(m)•f(n),令 m=n=0 可得 f(0)=f(0)f(0),
故有 f(0)=1.
(2)由f(m+n)=f(m)•f(n)可得 f(0)=f(x-x)=f(x)f(-x)=1,∴f(-x)=

,故f(x)与f(-x)互为倒数,故函数f(x)>0恒成立.
设 x
2>x
1,则 x
2-x
1>0,由题意可得 0<f(x
2-x
1)<1.
∴f(x
2)-f(x
1)=f(x
2-x
1+x
1)-f(x
1)=f(x
2-x
1)•f(x
1)-f(x
1)=f(x
1)[f(x
2-x
1)-1]<0,
故函数 f(x)在R上是减函数.
(3)A={(x,y)|f(x
2)f(y
2)>f(1)}={(x,y)|f(x
2+y
2)>f(1)}={(x,y)|x
2+y
2<1 },表示一个以原点为圆心、半径等于1的圆面(不包含边界).
B={(x,y)|f(ax-y+

)=f(0)}={(x,y)|ax-y+

=0 },表示一条过点(0,

)的一条直线.
若A∩B=∅,则圆和直线相切或相离,故有
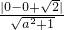
≥1,解得-1≤a≤1.
分析:(1)在f(m+n)=f(m)•f(n),令 m=n=0 可得f(0)=1.
(2)由f(m+n)=f(m)•f(n)可得 f(-x)=

,故f(x)与f(-x)互为倒数,故函数f(x)>0恒成立.再由 f(x
2)-f(x
1)=f(x
2-x
1+x
1)-f(x
1)=f(x
1)[f(x
2-x
1)-1]<0,可得函数 f(x)在R上是减函数.
(3)化简A为 {(x,y)|x
2+y
2<1 },表示一个以原点为圆心、半径等于1的圆面(不包含边界).化简B为 {(x,y)|ax-y+

=0 },表示一条过点(0,

)的一条直线.根据圆和直线相切或相离,可得
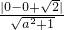
≥1,由此解得a的范围.
点评:本题主要考查函数的单调性的判断和证明,直线和圆的位置关系的应用,属于中档题.

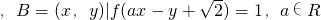 ,若A∩B=∅,试确定a的取值范围.
,若A∩B=∅,试确定a的取值范围. ,故f(x)与f(-x)互为倒数,故函数f(x)>0恒成立.
,故f(x)与f(-x)互为倒数,故函数f(x)>0恒成立. )=f(0)}={(x,y)|ax-y+
)=f(0)}={(x,y)|ax-y+ =0 },表示一条过点(0,
=0 },表示一条过点(0, )的一条直线.
)的一条直线.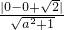 ≥1,解得-1≤a≤1.
≥1,解得-1≤a≤1. ,故f(x)与f(-x)互为倒数,故函数f(x)>0恒成立.再由 f(x2)-f(x1)=f(x2-x1+x1)-f(x1)=f(x1)[f(x2-x1)-1]<0,可得函数 f(x)在R上是减函数.
,故f(x)与f(-x)互为倒数,故函数f(x)>0恒成立.再由 f(x2)-f(x1)=f(x2-x1+x1)-f(x1)=f(x1)[f(x2-x1)-1]<0,可得函数 f(x)在R上是减函数. =0 },表示一条过点(0,
=0 },表示一条过点(0, )的一条直线.根据圆和直线相切或相离,可得
)的一条直线.根据圆和直线相切或相离,可得 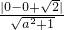 ≥1,由此解得a的范围.
≥1,由此解得a的范围.
