
 ,且OA=2,OB=1,则直线AB与平面OBC所成角的余弦值为 .
,且OA=2,OB=1,则直线AB与平面OBC所成角的余弦值为 .  可求,进而可求余弦值
可求,进而可求余弦值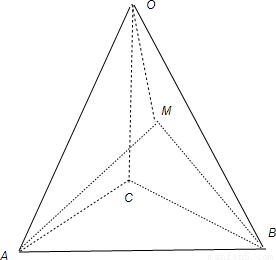 解:过A作AM⊥平面OBC,垂足为M,连接AM,BM
解:过A作AM⊥平面OBC,垂足为M,连接AM,BM


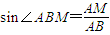 =
=


 ,可得OM在∠COB的角平分线上,②三余弦定理的应用是解决本题的另一个关键,只有知道该结论,才能求解出题目中的AM,进而可求所要求解的角.
,可得OM在∠COB的角平分线上,②三余弦定理的应用是解决本题的另一个关键,只有知道该结论,才能求解出题目中的AM,进而可求所要求解的角. 

 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com