
 +t3-3t(x∈R),其中|t|≤1,将f(x)的最小值记为g(t),则函数g(t)的单调递增区间为
+t3-3t(x∈R),其中|t|≤1,将f(x)的最小值记为g(t),则函数g(t)的单调递增区间为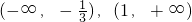

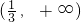

 的范围确定函数的最小值的表达式,即g(t)进而对函数进行求导,利用导函数大于0求得t的范围,即函数g(t)的递增区间.
的范围确定函数的最小值的表达式,即g(t)进而对函数进行求导,利用导函数大于0求得t的范围,即函数g(t)的递增区间. +t3-3t=4sin4
+t3-3t=4sin4 +(4t-4)sin2
+(4t-4)sin2 +t3-3t+1=4(sin2
+t3-3t+1=4(sin2 +
+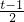 )2+t3-t2-t
)2+t3-t2-t ≤1
≤1 =-
=-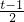 时函数有最小值为g(t)=t3-t2-t
时函数有最小值为g(t)=t3-t2-t 时,函数g(t)单调增.因为|t|≤1
时,函数g(t)单调增.因为|t|≤1 ;
;

 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com