
����Ŀ���ҹ�������������ȱˮ�Ĺ���֮һ������ȱˮ�����Ϊͻ����ij������Ϊ�˹��������Լ��ˮ���ƻ���������������ˮ�շѷ�������ȷ��һ������������ˮ����![]() (��)��һλ���������ˮ��������
(��)��һλ���������ˮ��������![]() �IJ��ְ�ƽ���շѣ�����
�IJ��ְ�ƽ���շѣ�����![]() �IJ��ְ�����շѣ�Ϊ���˽������ˮ�����ͨ�����飬�����ij��
�IJ��ְ�����շѣ�Ϊ���˽������ˮ�����ͨ�����飬�����ij��![]() λ�����˵��¾���ˮ��(��λ����)�������ݰ���
λ�����˵��¾���ˮ��(��λ����)�������ݰ���![]() �ֳ�
�ֳ�![]() �飬�Ƴ�����ͼ��ʾ��Ƶ�ʷֲ�ֱ��ͼ.
�飬�Ƴ�����ͼ��ʾ��Ƶ�ʷֲ�ֱ��ͼ.
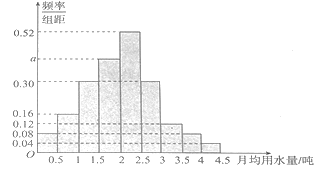
��1����ֱ��ͼ��![]() ��ֵ��
��ֵ��
��2����������![]() �������ȫ�о������¾���ˮ��������
�������ȫ�о������¾���ˮ��������![]() �ֵ���������˵�����ɣ�
�ֵ���������˵�����ɣ�
��3������������ϣ��ʹ![]() �ľ���ÿ�µ���ˮ����������
�ľ���ÿ�µ���ˮ����������![]() (��)������
(��)������![]() ��ֵ(��ȷ��
��ֵ(��ȷ��![]() )����˵������.
)����˵������.
 ÿ��10���ӿ�����������������ϵ�д�
ÿ��10���ӿ�����������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����p:ʵ��x����![]() ,����
,����![]() ,����
,����![]() ʵ��
ʵ��![]() ����
����
|x-3|��1 .
(1)��![]() ��
��![]() Ϊ�棬��ʵ��
Ϊ�棬��ʵ��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
(2)��![]() ��
��![]()
![]() �ij�ֲ���Ҫ����,��ʵ��a��ȡֵ��Χ.
�ij�ֲ���Ҫ����,��ʵ��a��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���躯��![]() ��
��
����������![]() �ڵ�
�ڵ�![]() �������߷��̣�
�������߷��̣�
������![]() ��
��![]() ���������ʵ��
���������ʵ��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
����������![]() ��ֵ��ʹ����
��ֵ��ʹ����![]() ������
������![]() ������㣮
������㣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С����С����λͬѧ�������ӣ������ʵؾ��ȣ���Ϸ������С������һö���ӣ����ϵĵ�����Ϊ![]() ��С�����һö���ӣ����ϵĵ�����Ϊ
��С�����һö���ӣ����ϵĵ�����Ϊ![]() .
.
��1����![]() �ܱ�
�ܱ�![]() �����ĸ���.
�����ĸ���.
��2���涨����![]() ����С��Ӯ����
����С��Ӯ����![]() ����С��Ӯ���������������Ӯ.���������Ϸ����ƽ����˵������.
����С��Ӯ���������������Ӯ.���������Ϸ����ƽ����˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=2cos2��x+2sin��xcos��x���أ�0������С������Ϊ�У�
������f��![]() ����ֵ��
����ֵ��
��������f��x���ĵ����������䣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪x0��x0+![]() �Ǻ���f��x��=cos2��wx��
�Ǻ���f��x��=cos2��wx��![]() ����sin2wx���أ�0�����������ڵ����
����sin2wx���أ�0�����������ڵ����
��1����![]() ��ֵ��
��ֵ��
��2����������![]() ������f��x����m��0����ʵ��m��ȡֵ��Χ��
������f��x����m��0����ʵ��m��ȡֵ��Χ��
��3��������![]() �ķ���
�ķ���![]() ��
��![]() ����������ͬ�Ľ⣬��ʵ��
����������ͬ�Ľ⣬��ʵ��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У���P�ǵ�λԲ�ϵĶ��㣬����P��x��Ĵ���������y=![]() x��x��0�����ڵ�Q����x�ύ�ڵ�M���ǡ�MOP=�����Ҧ��ʣ���
x��x��0�����ڵ�Q����x�ύ�ڵ�M���ǡ�MOP=�����Ҧ��ʣ���![]() ��
�� ![]() ����
����
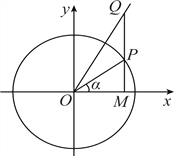
������sin��=![]() ����cos��POQ��
����cos��POQ��
�������OPQ��������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������С������12�֣�
��֪OΪ����ԭ�㣬����![]() ����P����
����P����![]() ��
��
�������Ǻ���![]() ��
��![]() ������
������![]() ����С�����ڣ�
����С�����ڣ�
��������O��P��C���㹲�ߣ���![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com