
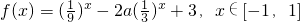
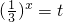 ,∵x∈[-1,1],∴
,∵x∈[-1,1],∴ ------------------------(1分)
------------------------(1分)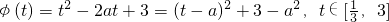 ------------(2分)
------------(2分) 时,
时,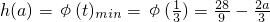 -------------(3分)
-------------(3分)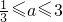 时,h(a)=φ(t)min=φ(a)=3-a2-------------(4分)
时,h(a)=φ(t)min=φ(a)=3-a2-------------(4分)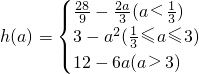 --------------(6分)
--------------(6分)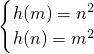 即:
即: -----(9分)
-----(9分)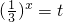 ,利用换元法,可将已知函数
,利用换元法,可将已知函数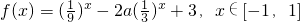 化为一个二次函数,根据二次函数在定区间上的最值问题,即可得到h(a)的解析式.
化为一个二次函数,根据二次函数在定区间上的最值问题,即可得到h(a)的解析式.

 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案科目:高中数学 来源:2011年北京市石景山区高考数学一模试卷(文科)(解析版) 题型:解答题
 .
.查看答案和解析>>
科目:高中数学 来源:2012-2013学年河南省郑州一中高一(上)期中数学试卷(解析版) 题型:解答题
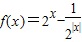 .
.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com