
 的单调递减区间是
的单调递减区间是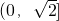

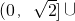

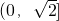 和
和
 ,分两种情况进行讨论可以得到函数的单调区间,要注意两个单调减区间
,分两种情况进行讨论可以得到函数的单调区间,要注意两个单调减区间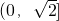 ,
, ,不能写成
,不能写成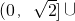
 的形式
的形式 )-(
)-( )
) -
- )
)
 时,x1•x2-2<0,所以
时,x1•x2-2<0,所以 <0
<0 ]上是减函数.
]上是减函数. ,0)上也是减函数.
,0)上也是减函数. 和-
和- ≤x1<x2<0进行讨论.
≤x1<x2<0进行讨论. 

 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com