
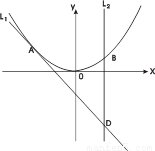
已知A(-1,2)为抛物线C: y=2x2上的点,直线![]() 过点A,且与抛物线C 相切,直线
过点A,且与抛物线C 相切,直线![]() :x=a(a≠-1)交抛物线C于B,交直线
:x=a(a≠-1)交抛物线C于B,交直线![]() 于点D.
于点D.
(1)求直线![]() 的方程.
的方程.
(2)设![]() 的面积为S1,求
的面积为S1,求![]() 及S1的值.
及S1的值.
(3)设由抛物线C,直线![]() 所围成的图形的面积为S2,求证S1:S2的值为与a无关的常数.
所围成的图形的面积为S2,求证S1:S2的值为与a无关的常数.
(1)![]() 的方程为y-2=-4(x+1)即y=-4x-2 (2)
的方程为y-2=-4(x+1)即y=-4x-2 (2) ![]() = 2
= 2![]() 2+4
2+4![]() +2=2(
+2=2(![]() +1)2
+1)2
∴S1=![]() (3) S1:S2的值为与
(3) S1:S2的值为与![]() 无关的常数,这常数是
无关的常数,这常数是![]()
(1)由![]() 当x=1时,y'=-4 ……………2分
当x=1时,y'=-4 ……………2分
∴![]() 的方程为y-2=-4(x+1)即y=-4x-2 ……………………3分
的方程为y-2=-4(x+1)即y=-4x-2 ……………………3分
(2)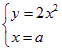 得B点坐标为(
得B点坐标为(![]() ) ……………………4分
) ……………………4分
由![]() 得D点坐标(
得D点坐标(![]() ,-4
,-4![]() -2) ……………………5分
-2) ……………………5分
点A 到直线BD的距离为![]() ………………………………6分
………………………………6分
![]() = 2
= 2![]() 2+4
2+4![]() +2=2(
+2=2(![]() +1)2
+1)2
∴S1=![]() ………………………………7分
………………………………7分
(3)当![]() >-1时,S1=(
>-1时,S1=(![]() +1)3, ………………………………………8分
+1)3, ………………………………………8分

…………………………………………9分
…………………………………………10分
∴S1:S2=![]() ………………………………………………………………………11分
………………………………………………………………………11分
当![]() <-1时,S1= -(
<-1时,S1= -(![]() +1)3 ……………………………………………………12
+1)3 ……………………………………………………12
 ……………………………………………13分
……………………………………………13分
∴S1:S2=![]()
综上可知S1:S2的值为与![]() 无关的常数,这常数是
无关的常数,这常数是![]() …………………………………14分
…………………………………14分


 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案科目:高中数学 来源: 题型:
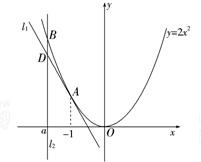 已知A(-1,2)为抛物线C:y=2x2上的点,直线l1过点A,且与抛物线C相切,直线l2:x=a(a<-1)交抛物线C于点B,交直线l1于点D.
已知A(-1,2)为抛物线C:y=2x2上的点,直线l1过点A,且与抛物线C相切,直线l2:x=a(a<-1)交抛物线C于点B,交直线l1于点D.查看答案和解析>>
科目:高中数学 来源: 题型:
| x2 |
| 4 |
| y2 |
| 16 |
| A、x+2y+4=0 |
| B、x+2y-4=0 |
| C、2x+y+4=0 |
| D、2x+y-4=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:
已知A(-1,2)为抛物线C:y=2x2上一点,直线l1过点A,且与抛物线C相切,直线l2:x=a(a≠-1)交抛物线C于B,交l1于D.
(1)求直线l1的方程;(2)设△ABD的面积为S,求|BD|及S的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知A(-1,2)为抛物线C:y=2x2上的点,直线l1过点A且与抛物线C相切,直线l2:x=a(a<-1)交抛物线C 于点B,交直线l1于点D.
(1)求直线l1的方程;
(2)求△ABD的面积S1;
(3)求由抛物线C及直线l1和直线l2所围成的图形面积S2.
查看答案和解析>>
科目:高中数学 来源:2013届广东省高二下学期第一次月考理科数学试卷 题型:解答题
(本小题满分14分)
已知A(-1,2)为抛物线C: y=2x2上的点,直线 过点A,且与抛物线C 相切,直线
过点A,且与抛物线C 相切,直线 :x=a(a≠-1)交抛物线C于B,交直线
:x=a(a≠-1)交抛物线C于B,交直线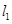 于点D.
于点D.
(1)求直线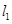 的方程.
的方程.
(2)设 的面积为S1,求
的面积为S1,求 及S1的值.
及S1的值.
(3)设由抛物线C,直线 所围成的图形的面积为S2,求证S1:S2的值为与a无关的常数.
所围成的图形的面积为S2,求证S1:S2的值为与a无关的常数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com