
解:(1)甲从1到m(m为给定的正整数,且2≤m≤n-2)号中任选两款,乙从(m+1)到n号中任选两款的所有等可能基本事件的种数为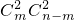 ,
,
记“款式s和t(1≤s≤m,m+1≤t≤n)同时被选中”为事件B,则事件B包含的基本事件的种数为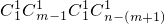 ,
,
所以P(B)=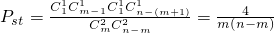 ,
,
则所有的Pst的和为: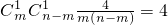
(2)甲从n种不同款式的服装中选取服装的所有可能种数为: =2n,
=2n,
同理得,乙从n种不同款式的服装中选取服装的所有可能种数为2n,
据分步乘法计数原理得,所有等可能的基本事件的种数为:2n•2n=4n,
记“至少有一个款式为甲和乙共同认可”为事件A,则事件A的对立事件 为:“没有一个款式为甲和乙共同认可”,
为:“没有一个款式为甲和乙共同认可”,
而事件 包含的基本事件种数为:
包含的基本事件种数为: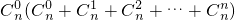 +
+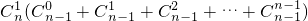 +…+
+…+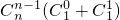
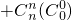 =
=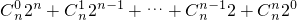 =(1+2)n=3n,
=(1+2)n=3n,
所以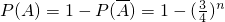


 中考解读考点精练系列答案
中考解读考点精练系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2012-2013学年江苏省盐城中学高三(下)开学数学试卷(解析版) 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2012年江苏省南通市教研室高考数学全真模拟试卷(四)(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com