练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    老师告诉学生小明说，“若O为△ABC所在平面上的任意一点，且有等式
    OP
    =
    OA
    +λ(
    AB
    cosC
    |
    AB
    |
    +
    AC
    cosB
    |
    AC
    |
    )    ，则P点的轨迹必过△ABC的垂心”，小明进一步思考何时P点的轨迹会通过△ABC的外心，得到的条件等式应为
    OP
    =
    OP
    =
    OB
    +
    OC
    2
    +λ(
    AB
    |
    AB
    |cosB
    +
    AC
    |
    AC
    |cosC
    )
    OP
    =
    OB
    +
    OC
    2
    +λ(
    AB
    |
    AB
    |cosB
    +
    AC
    |
    AC
    |cosC
    )
    ．（用O，A，B，C四个点所构成的向量和角A，B，C的三角函数以及λ表示）
    分析：由题意可得：
    BC
    •（
    AB
    |
    AB
    | cosB
    +
    AC
    |
    AC
    | cosC
    ）=0，即 
    BC
    与λ（
    AB
    |
    AB
    | cosB
    +
    AC
    |
    AC
    | cosC
    ）垂直，设D为BC的中点，则
    OB
    +
    OC
    2
    =
    OD
    ，可得λ（
    AB
    |
    AB
    | cosB
    +
    AC
    |
    AC
    | cosC
    ）=
    DP
    ，即可得到
    BC
    •
    DP
    =0    ，进而得到点P在BC的垂直平分线上，即可得到答案．
    解答：解：由题意可得：
    BC
    •（
    AB
    |
    AB
    | cosB
    +
    AC
    |
    AC
    | cosC
    ）=-|
    BC
    |+|
    BC
    |=0
    ∴
    BC
    与λ（
    AB
    |
    AB
    | cosB
    +
    AC
    |
    AC
    | cosC
    ）垂直
    设D为BC的中点，则
    OB
    +
    OC
    2
    =
    OD
    ，
    所以
    OP
    =
    OB
    +
    OC
    2
    +λ(
    AB
    |
    AB
    |cosB
    +
    AC
    |
    AC
    |cosC
    )    ，即
    OP
    =
    OD
    +λ(
    AB
    |
    AB
    |cosB
    +
    AC
    |
    AC
    |cosC
    )    ，
    所以λ（
    AB
    |
    AB
    | cosB
    +
    AC
    |
    AC
    | cosC
    ）=
    DP
    ，
    因为
    BC
    与λ（
    AB
    |
    AB
    | cosB
    +
    AC
    |
    AC
    | cosC
    ）垂直
    所以
    BC
    •
    DP
    =0    ，
    又∵点D为BC的中点，
    ∴点P在BC的垂直平分线上，即P的轨迹会通过△ABC的外心．
    故答案为：
    OP
    =
    OB
    +
    OC
    2
    +λ(
    AB
    |
    AB
    |cosB
    +
    AC
    |
    AC
    |cosC
    )    ．
    点评：本题主要借助于类比推理重点考查了平面向量的加减法运算与数量积运算，并且也考查了三角形的五心等知识点，属于中档题．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：不详 题型：填空题

    老师告诉学生小明说，“若O为△ABC所在平面上的任意一点，且有等式
    OP
    =
    OA
    +λ(
    AB
    cosC
    |
    AB
    |
    +
    AC
    cosB
    |
    AC
    |
    )    ，则P点的轨迹必过△ABC的垂心”，小明进一步思考何时P点的轨迹会通过△ABC的外心，得到的条件等式应为
    OP
    =______．（用O，A，B，C四个点所构成的向量和角A，B，C的三角函数以及λ表示）

    查看答案和解析>>

    科目：高中数学 来源：2008年上海市上海中学高三3月综合练习数学试卷1（文理合卷）（解析版） 题型：解答题

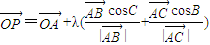    老师告诉学生小明说，“若O为△ABC所在平面上的任意一点，且有等式，则P点的轨迹必过△ABC的垂心”，小明进一步思考何时P点的轨迹会通过△ABC的外心，得到的条件等式应为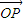=    ．（用O，A，B，C四个点所构成的向量和角A，B，C的三角函数以及λ表示）

    查看答案和解析>>

    科目：高中数学 来源：2010年上海市上海中学高三数学综合练习试卷（1）（解析版） 题型：解答题

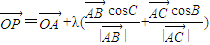    老师告诉学生小明说，“若O为△ABC所在平面上的任意一点，且有等式，则P点的轨迹必过△ABC的垂心”，小明进一步思考何时P点的轨迹会通过△ABC的外心，得到的条件等式应为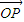=    ．（用O，A，B，C四个点所构成的向量和角A，B，C的三角函数以及λ表示）

    查看答案和解析>>

    同步练习册答案