
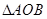 中,
中,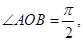 AB=2OB=4,D为AB的中点,若
AB=2OB=4,D为AB的中点,若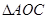 是
是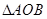 绕直线AO旋转而成的,记二面角B—AO—C的大小为
绕直线AO旋转而成的,记二面角B—AO—C的大小为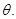 (I)若
(I)若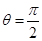 ,求证:平面
,求证:平面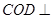 平面AOB;(II)若
平面AOB;(II)若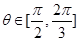 时,求二面角C—OD—B的余弦值的最小值。
时,求二面角C—OD—B的余弦值的最小值。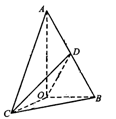
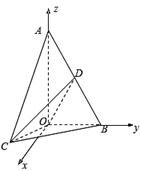
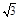 ),B(0,2,0),D(0,1,
),B(0,2,0),D(0,1,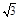 ),C(2sinθ,2cosθ,0).
),C(2sinθ,2cosθ,0).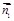 =(x,y,z)为平面COD的一个法向量,
=(x,y,z)为平面COD的一个法向量,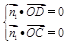 ,得
,得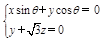 ,……3分
,……3分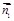 =(
=(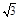 cosθ,-
cosθ,-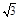 sinθ,sinθ)=(0,-
sinθ,sinθ)=(0,-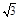 ,1)
,1)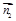 =(1,0,0),得
=(1,0,0),得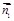 ·
·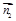 =0,
=0,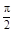 时,cosα=0;当θ∈(
时,cosα=0;当θ∈(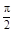 ,
,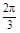 ]时,tanθ≤-
]时,tanθ≤-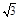 ,
,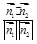 =
= =-
=-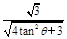 ,……10分
,……10分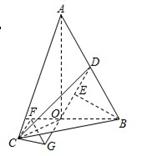
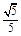 ≤cosα<0.因此cosα的最小值为-
≤cosα<0.因此cosα的最小值为-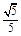 ,
,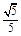 . ……12分
. ……12分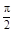 , ……3分
, ……3分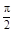 时,二面角C-OD-B的余弦值为0;……7分
时,二面角C-OD-B的余弦值为0;……7分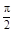 ,
,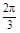 ]时,过B作OD的垂线,垂足为E,
]时,过B作OD的垂线,垂足为E,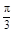 =-
=-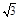 cosθ,CG=
cosθ,CG= ,
,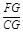 =-
=-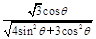 .因为θ∈(
.因为θ∈(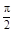 ,
,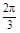 ],tanθ≤-
],tanθ≤-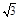 ,故0<cos∠CGF=
,故0<cos∠CGF=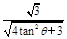 ≤
≤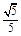 .所以二面角C-OD-B的余弦值的最小值为-
.所以二面角C-OD-B的余弦值的最小值为-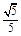 . ……12分
. ……12分

 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案科目:高中数学 来源:不详 题型:单选题
 中,有一半球,其底面与正三棱锥的底面重合,正三棱锥的三个侧面都和半球相切。如果半球的半径等于1,则当正三棱锥的体积最小时,正三棱锥的高等于( )
中,有一半球,其底面与正三棱锥的底面重合,正三棱锥的三个侧面都和半球相切。如果半球的半径等于1,则当正三棱锥的体积最小时,正三棱锥的高等于( )A.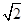 | B.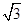 | C.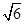 | D.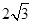 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
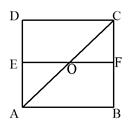
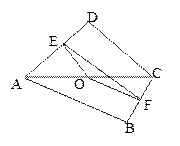
 是边长为
是边长为 的正方形
的正方形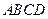 的中心,点
的中心,点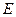 、
、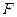 分别是
分别是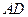 、
、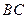 的中点,沿对角线
的中点,沿对角线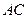 把正方形
把正方形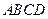 折成直二面角
折成直二面角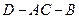 ;
;
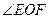 的大小;
的大小;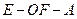 的余弦值;
的余弦值;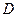 到面
到面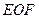 的距离.
的距离.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
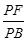 =
=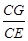 =λ∈(0,1).
=λ∈(0,1).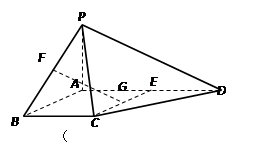
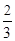 .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题


查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
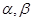 为两个不重合的平面,
为两个不重合的平面,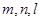 是不重合的直线,给出下列命题,其中正确的序号是 ▲
是不重合的直线,给出下列命题,其中正确的序号是 ▲ 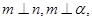 则
则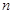 ∥
∥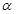 ;② 若
;② 若
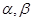 相交不垂直,则n与m不垂直;③ 若
相交不垂直,则n与m不垂直;③ 若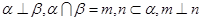 ,则
,则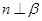 ;④ m是平面
;④ m是平面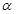 的斜线,n是m在平面
的斜线,n是m在平面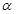 内的射影,若
内的射影,若 ,则
,则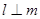 .
.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com