
 和
和  线性相关 等价于
线性相关 等价于  和
和  是共线向量,故①正确,②不正确,④正确.通过举反例可得③不正确.
是共线向量,故①正确,②不正确,④正确.通过举反例可得③不正确. 、
、 线性相关,假设λ≠0,则
线性相关,假设λ≠0,则 =-
=-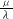
 ,故
,故  和
和  是共线向量.
是共线向量. 和
和  是共线向量,则
是共线向量,则  =-
=-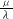
 ,即λ
,即λ +μ
+μ =0,故
=0,故  和
和  线性相关.
线性相关. 和
和  线性相关 等价于
线性相关 等价于  和
和  是共线向量.
是共线向量. =2
=2  ,则
,则  -2
-2  =0,故
=0,故  和
和  线性相关,故①正确.
线性相关,故①正确. 和
和  为非零向量,
为非零向量, ⊥
⊥ ,则
,则  和
和  不是共线向量,不能推出
不是共线向量,不能推出 和
和  线性相关,故②不正确.
线性相关,故②不正确. 和
和  线性相关,则
线性相关,则  和
和  线性相关,不能推出若
线性相关,不能推出若 和
和  线性相关,例如当
线性相关,例如当 =
= 时,
时, 和
和  可以是任意的两个向量.故③不正确.
可以是任意的两个向量.故③不正确. 和
和  线性相关的充要条件是
线性相关的充要条件是  和
和  是共线向量,故④正确.
是共线向量,故④正确. 和
和  线性相关 等价于
线性相关 等价于  和
和  是共线向量,是解题的关键.
是共线向量,是解题的关键. 

 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| c |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| b |
| c |
| a |
| c |
| a |
| b |
| a |
| b |
查看答案和解析>>
科目:高中数学 来源:2010-2011学年四川省高三普通高考考生知识能力水平摸底考试数学理卷 题型:填空题
设a、b为平面向量,若存在不全为零的实数 使得
使得 ,则除a、b线性相关,下面的命题中,a、b、c均为已知平面M上的向量。
,则除a、b线性相关,下面的命题中,a、b、c均为已知平面M上的向量。
①若a=2b,则a、b线性相关;
②若a、b为非零向量,且 ,则a、b线性相关;
,则a、b线性相关;
③若a、b线性相关,b、c线性相关,则a、c线性相关;
④向量a、b线性相关的充要条件是a、b共线。
上述命题中正确的是 (写出所有正确命题的编号)
查看答案和解析>>
科目:高中数学 来源:2010-2011学年四川省高三普通高考考生知识能力水平摸底考试数学理卷 题型:填空题
设a、b为平面向量,若存在不全为零的实数 使得
使得 ,则除a、b线性相关,下面的命题中,a、b、c均为已知平面M上的向量。
,则除a、b线性相关,下面的命题中,a、b、c均为已知平面M上的向量。
①若a=2b,则a、b线性相关;
②若a、b为非零向量,且 ,则a、b线性相关;
,则a、b线性相关;
③若a、b线性相关,b、c线性相关,则a、c线性相关;
④向量a、b线性相关的充要条件是a、b共线。
上述命题中正确的是 (写出所有正确命题的编号)
查看答案和解析>>
科目:高中数学 来源:2011届四川省高三普通高考考生知识能力水平摸底考试数学理卷 题型:填空题
设a、b为平面向量,若存在不全为零的实数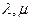 使得
使得 ,则除a、b线性相关,下面的命题中,a、b、c均为已知平面M上的向量。
,则除a、b线性相关,下面的命题中,a、b、c均为已知平面M上的向量。
①若a=2b,则a、b线性相关;
②若a、b为非零向量,且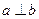 ,则a、b线性相关;
,则a、b线性相关;
③若a、b线性相关,b、c线性相关,则a、c线性相关;
④向量a、b线性相关的充要条件是a、b共线。
上述命题中正确的是 (写出所有正确命题的编号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com