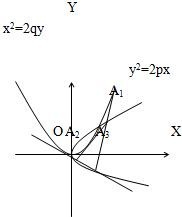
分析:设p>0,q>0.又设y2=2px的内接三角形顶点为A1(x1,y1),A2(x2,y2),A3(x3,y3),分别代入抛物线方程,依题意,设A1A2,A2A3与抛物线x2=2qy相切,要证A3A1也与抛物线x2=2qy相切,由x2=2qy在原点O处的切线是y2=2px的对称轴,可知原点O不能是所设内接三角形的顶点推断三个顶点都不能是(0,0);故可设直线A1A2的方程,进而得A1A2方程代入抛物线方程,整理后根据判别式等于0,求得2p2q+y1y2(y1+y2)=0同理由于A2A3与抛物线x2=2qy相切,A2A3也不能与Y轴平行,即x2≠x3,y2≠-y3,同样得到2p2q+y2y3(y2+y3)=0把y2=-y1-y3代入2p2q+y1y2(y1+y2)=0整理后可说明A3A1与抛物线x2=2qy的两个交点重合,进而可判断只要A1A2,A2A3与抛物线x2=2qy相切,则A3A1也与抛物线x2=2qy相切.
解答:解:不失一般性,设p>0,q>0.又设y
2=2px的内接三角形顶点为
A
1(x
1,y
1),A
2(x
2,y
2),A
3(x
3,y
3)
因此y
12=2px
1,y
22=2px
2,y
32=2px
3其中y
1≠y
2,y
2≠y
3,y
3≠y
1.
依题意,设A
1A
2,A
2A
3与抛物线x
2=2qy相切,
要证A
3A
1也与抛物线x
2=2qy相切
因为x
2=2qy在原点O处的切线是y
2=2px的对称轴,
所以原点O不能是所设内接三角形的顶点
即(x
1,y
1),(x
2,y
2),(x
3,y
3),
都不能是(0,0);又因A
1A
2与x
2=2qy相切,
所以A
1A
2不能与Y轴平行,即x
1≠x
2,y
1≠-y
2,
直线A
1A
2的方程是
y-y1=(x-x1),
∵y
22-y
12=(y
2-y
1)(y
2+y
1)=2p(x
2-x
1).
∴A
1A
2方程是y=
x+.A
1A
2与抛物线x
2=2qy交点的横坐标满足
x2-x-=0,
由于A
1A
2与抛物线x
2=2qy相切,上面二次方程的判别式
△=
(-)2+4()=0.
化简得2p
2q+y
1y
2(y
1+y
2)=0(1)
同理由于A
2A
3与抛物线x
2=2qy相切,A
2A
3也不能与Y轴平行,即
x
2≠x
3,y
2≠-y
3,同样得到2p
2q+y
2y
3(y
2+y
3)=0(2)
由(1)(2)两方程及y
2≠0,y
1≠y
3,得y
1+y
2+y
3=0.
由上式及y
2≠0,得y
3≠-y
1,也就是A
3A
1也不能与Y轴平行
今将y
2=-y
1-y
3代入(1)式得:2p
2q+y
3y
1(y
3+y
1)=0(3)
(3)式说明A
3A
1与抛物线x
2=2qy的两个交点重合,
即A
3A
1与抛物线x
2=2qy相切
所以只要A
1A
2,A
2A
3与抛物线x
2=2qy相切,
则A
3A
1也与抛物线x
2=2qy相切.
点评:本题主要考查抛物线的应用和直线与抛物线的关系.考查了学生综合分析问题和运算能力.



 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案