解:(1)

=cos2x
∵
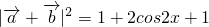
=2(1+cos2x)=4cos
2x
∴

x

(2)∵

=cos2x-8cosx=2cos
2x-8cosx-1=2(cosx-2)
2-9
∵

∴cosx∈[0,1]∴f(x)∈[-7,-1]
(3)∵g(x)+2=0
∴cos2x+2tcosx+2=0
即2cos
2x+2tcosx+1=0
令cosx=μ∈[0,1),F(μ)=2μ
2+2tμ+1
∴
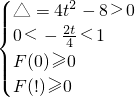
∴
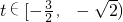
分析:(1)由向量的数量积的坐标表示及两角和的余弦公式可求

;根据平面向量的数量积 的性质可知,要求

,只要先求

,根据向量的运算可求
(2)由

=cos2x-8cosx=2cos
2x-8cosx-1=2(cosx-2)
2-9结合

可得cosx∈[0,1]从而可求f(x)
(3)g(x)+2=0?cos2x+2tcosx+2=0?2cos
2x+2tcosx+1=0有两不同解,
令cosx=μ∈[0,1),F(μ)=2μ
2+2tμ+1在[0,1)上有两不同解
结合方程的实根分布可得
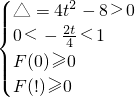
解不等式可得
点评:平面向量与三角函数结合的试题一般是利用平面向量为工具,转化为三角函数的 形式,利用三角的知识求解函数的最值(或值域),而以三角形式出现的二次函数要在求最值时要注意范围的限制条件

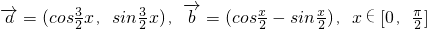
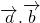 及
及 ;
;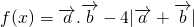 的值域;
的值域;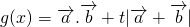 ,若关于x的方程g(x)+2=0有两不同解,求t的取值范围?.
,若关于x的方程g(x)+2=0有两不同解,求t的取值范围?. =cos2x
=cos2x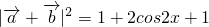 =2(1+cos2x)=4cos2x
=2(1+cos2x)=4cos2x x
x
 =cos2x-8cosx=2cos2x-8cosx-1=2(cosx-2)2-9
=cos2x-8cosx=2cos2x-8cosx-1=2(cosx-2)2-9 ∴cosx∈[0,1]∴f(x)∈[-7,-1]
∴cosx∈[0,1]∴f(x)∈[-7,-1]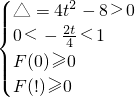
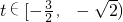
 ;根据平面向量的数量积 的性质可知,要求
;根据平面向量的数量积 的性质可知,要求
 ,根据向量的运算可求
,根据向量的运算可求 =cos2x-8cosx=2cos2x-8cosx-1=2(cosx-2)2-9结合
=cos2x-8cosx=2cos2x-8cosx-1=2(cosx-2)2-9结合 可得cosx∈[0,1]从而可求f(x)
可得cosx∈[0,1]从而可求f(x)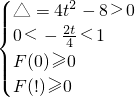 解不等式可得
解不等式可得

 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案


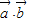 及
及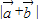 ;
;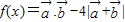 的值域;
的值域;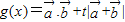 ,若关于x的方程g(x)+2=0有两不同解,求t的取值范围?.
,若关于x的方程g(x)+2=0有两不同解,求t的取值范围?.