
【题目】在平面直角坐标系xOy中,抛物线C的顶点是原点,以x轴为对称轴,且经过点P(1,2). (Ⅰ)求抛物线C的方程;
(Ⅱ)设点A,B在抛物线C上,直线PA,PB分别与y轴交于点M,N,|PM|=|PN|.求直线AB的斜率.
【答案】解:(Ⅰ)依题意,设抛物线C的方程为y2=ax(a≠0).
由抛物线C经过点P(1,2),
得a=4,
所以抛物线C的方程为y2=4x.
(Ⅱ)因为|PM|=|PN|,
所以∠PMN=∠PNM,
所以∠1=∠2,
所以直线PA与PB的倾斜角互补,
所以kPA+kPB=0.
依题意,直线AP的斜率存在,设直线AP的方程为:y﹣2=k(x﹣1)(k≠0),
将其代入抛物线C的方程,整理得k2x2﹣2(k2﹣2k+2)x+k2﹣4k+4=0.
设A(x1,y1),则x1= ![]() ,y1=
,y1= ![]() ﹣2,
﹣2,
所以A( ![]() ,
, ![]() ﹣2).
﹣2).
以﹣k替换点A坐标中的k,得B( ![]() ,﹣
,﹣ ![]() ﹣2.
﹣2.
所以 kAB=  =﹣1,
=﹣1,
所以直线AB的斜率为﹣1.
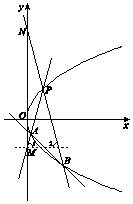
【解析】(Ⅰ)根据抛物线C经过点P(1,2),求抛物线C的方程;(Ⅱ)由题意,直线PA与PB的倾斜角互补,所以kPA+kPB=0,求出A,B的坐标,即可得出结论.


 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() x3﹣ax,在x=
x3﹣ax,在x= ![]() 处取得极小值,记g(x)=
处取得极小值,记g(x)= ![]() ,程序框图如图所示,若输出的结果S>
,程序框图如图所示,若输出的结果S> ![]() ,则判断框中可以填入的关于n的判断条件是( )
,则判断框中可以填入的关于n的判断条件是( ) 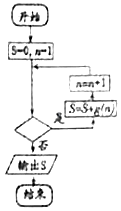
A.n≤12?
B.n>12?
C.n≤13?
D.n>13?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1所示,在等腰梯形ABCD中, ![]() .把△ABE沿BE折起,使得
.把△ABE沿BE折起,使得 ![]() ,得到四棱锥A﹣BCDE.如图2所示.
,得到四棱锥A﹣BCDE.如图2所示. 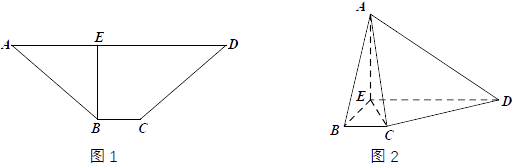
(1)求证:面ACE⊥面ABD;
(2)求平面ABE与平面ACD所成锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() ,其中a∈R. (Ⅰ)给出a的一个取值,使得曲线y=f(x)存在斜率为0的切线,并说明理由;
,其中a∈R. (Ⅰ)给出a的一个取值,使得曲线y=f(x)存在斜率为0的切线,并说明理由;
(Ⅱ)若f(x)存在极小值和极大值,证明:f(x)的极小值大于极大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】等比数列{an}的各项均为正数,且 ![]() .
.
(1)求数列{an}的通项公式;
(2)设bn=log3a1+log3a2+…+log3an , 求数列 ![]() 的前n项和Tn .
的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为2,O为AD的中点,射线OP从OA出发,绕着点O顺时针方向旋转至OD,在旋转的过程中,记∠AOP为x(x∈[0,π]),OP所经过的在正方形ABCD内的区域(阴影部分)的面积S=f(x),那么对于函数f(x)有以下三个结论,其中不正确的是( )
①f( ![]() )=
)= ![]()
②函数f(x)在( ![]() ,π)上为减函数
,π)上为减函数
③任意x∈[0, ![]() ],都有f(x)+f(π﹣x)=4.
],都有f(x)+f(π﹣x)=4.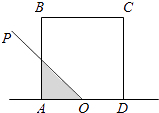
A.①
B.③
C.②
D.①②③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() ,点P(4,0),过右焦点F作与y轴不垂直的直线l交椭圆C于A,B两点. (Ⅰ)求椭圆C的离心率;
,点P(4,0),过右焦点F作与y轴不垂直的直线l交椭圆C于A,B两点. (Ⅰ)求椭圆C的离心率;
(Ⅱ)求证:以坐标原点O为圆心与PA相切的圆,必与直线PB相切.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com