
分析 (Ⅰ)由A与B,求出A∩B,A∪B即可;
(Ⅱ)求出B的补集,根据B补集与N的并集为R,求出a的范围即可.
解答 解:(Ⅰ)∵A={x|-4<x≤7},B={x|-5≤x<6},
∴A∩B={x|-4<x<6},A∪B={x|-5≤x≤7};
(Ⅱ)∵B={x|-5≤x<6},
∴∁UB={x|x<-5或x≥6},
∵(∁UB)∪N=R,N={x|a-4<x<a+8},
∴$\left\{\begin{array}{l}{a-4<-5}\\{a+8≥6}\end{array}\right.$,
解得:-2≤a<-1,
则实数a的范围为{a|-2≤a<-1}.
点评 此题考查了交、并、补集的混合运算,并集及其运算,以及交集及其运算,熟练掌握各自的定义是解本题的关键.


科目:高中数学 来源: 题型:选择题
 一天,小亮看到家中的塑料桶中有一个竖直放置的玻璃杯,桶子和玻璃杯的形状都是圆柱形,桶口的半径是杯口半径的2倍,其主视图如左图所示.小亮决定做个试验:把塑料桶和玻璃杯看作一个容器,对准杯口匀速注水,注水过程中杯子始终竖直放置,则下列能反映容器最高水位h与注水时间t之间关系的大致图象是( )
一天,小亮看到家中的塑料桶中有一个竖直放置的玻璃杯,桶子和玻璃杯的形状都是圆柱形,桶口的半径是杯口半径的2倍,其主视图如左图所示.小亮决定做个试验:把塑料桶和玻璃杯看作一个容器,对准杯口匀速注水,注水过程中杯子始终竖直放置,则下列能反映容器最高水位h与注水时间t之间关系的大致图象是( )| A. |  | B. |  | ||
| C. |  | D. | 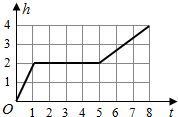 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(3)<f(1)<f(2) | B. | f(1)<f(2)<f(3) | C. | f(2)<f(1)<f(3) | D. | f(3)<f(2)<f(1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 9 | C. | -3 | D. | ±3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com